Programming Assignment 1: Representing, Managing and Manipulating Travel Options

You may NOT do any of the following:

• change any of the function names or signatures (parameter lists and types and return type)

• introduce any global or static variables

• use any arrays or vectors inside the TravelOptions class! Not for this assignment!! (You may use them as you see fit in any driver/tester programs you write)

You MAY do any of the following as you see fit:

• Introduce helper functions. But you should make them private.

Reminders: Some functions eliminate list entries (e.g., prune_sorted). Don't forget to deallocate the associated nodes (using the delete operator).

Bellow is the screen shot of code, Please read carefully and write the missing parts labeled as TO DO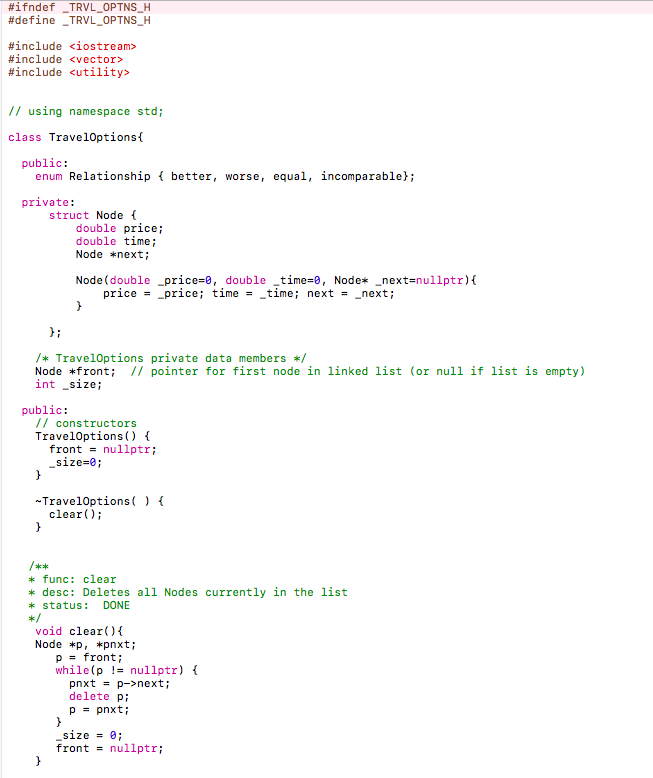

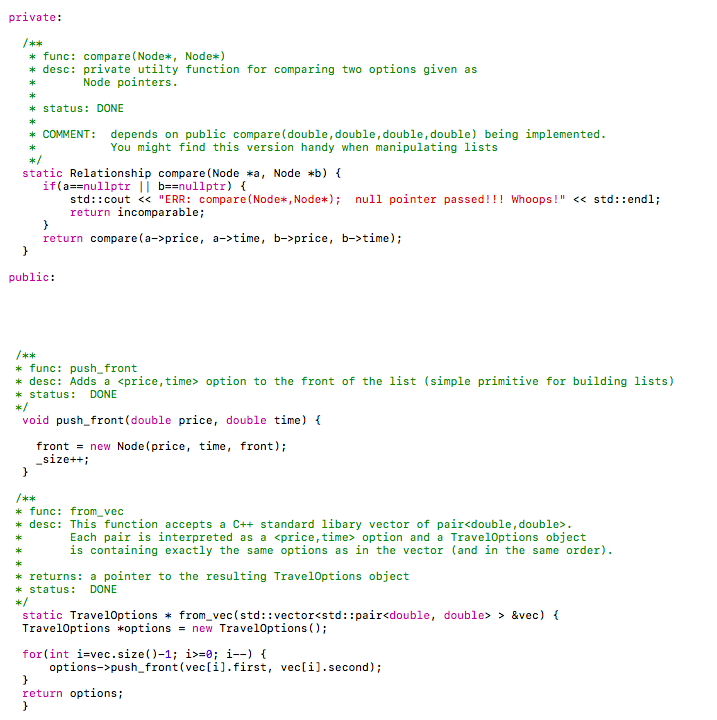
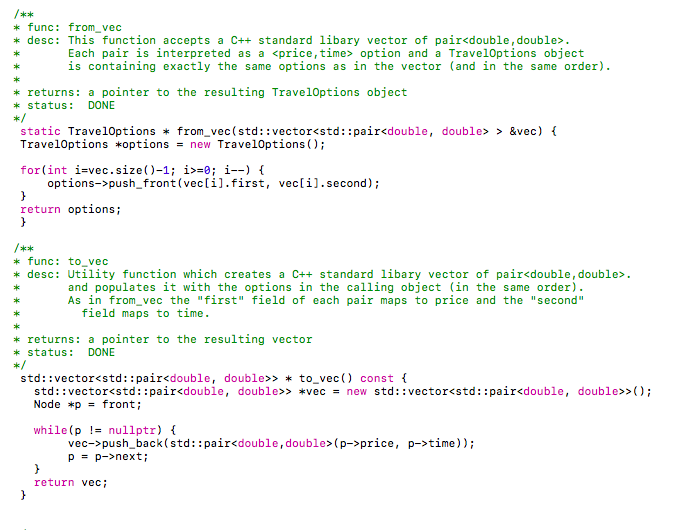
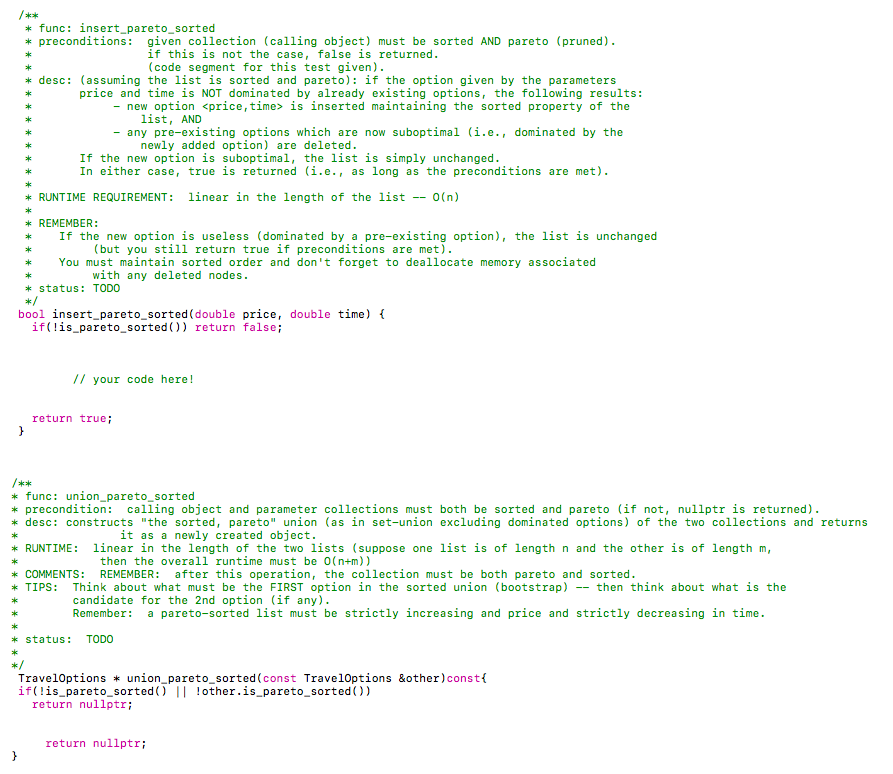
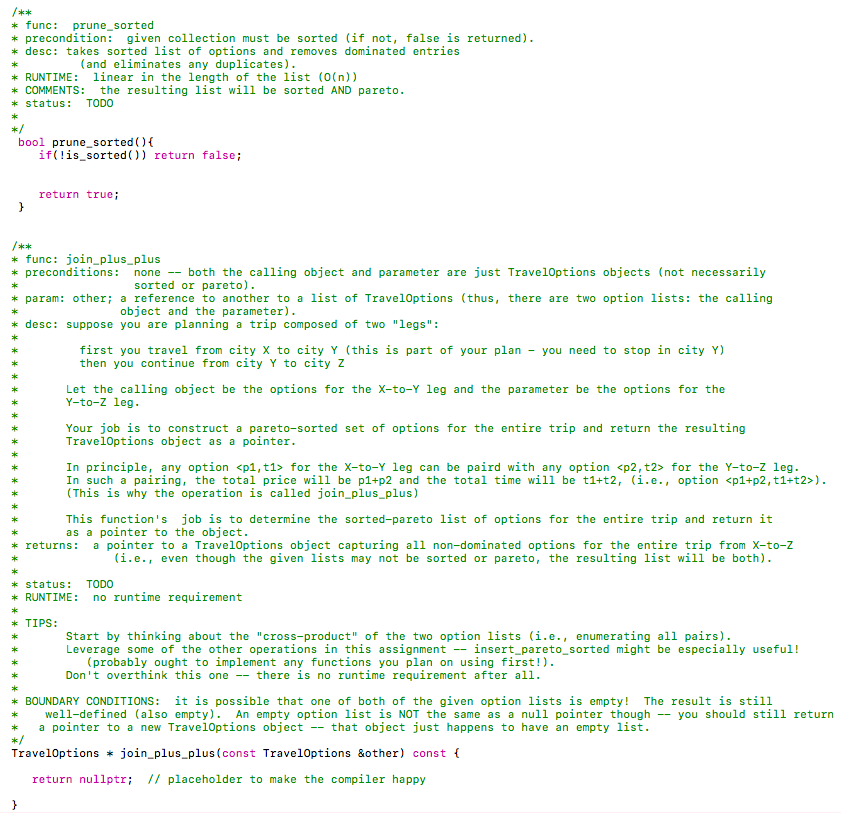
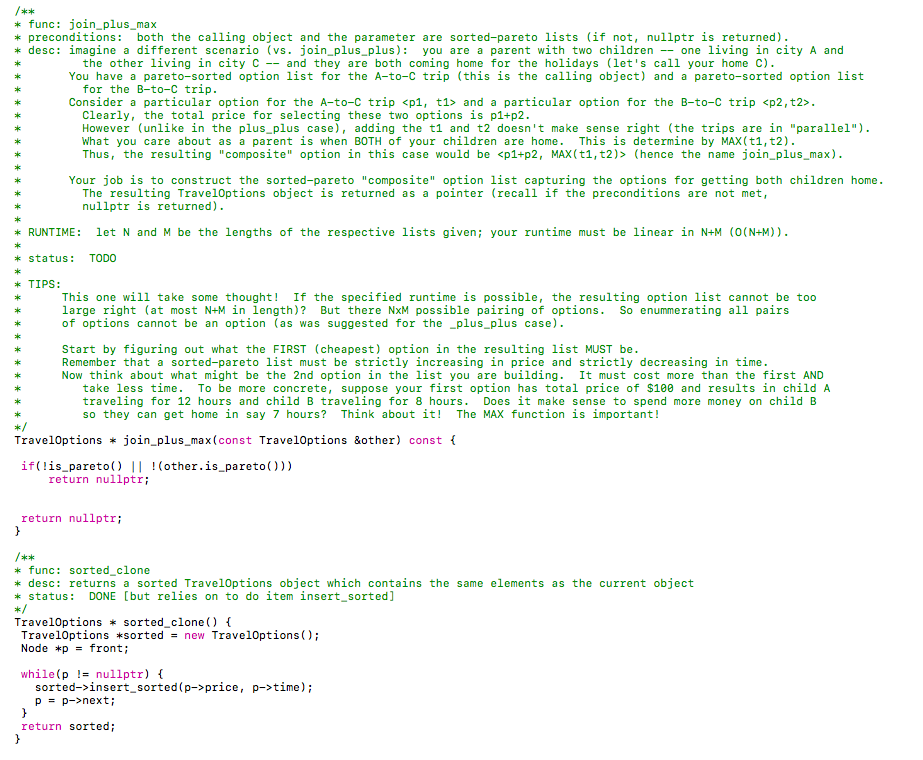
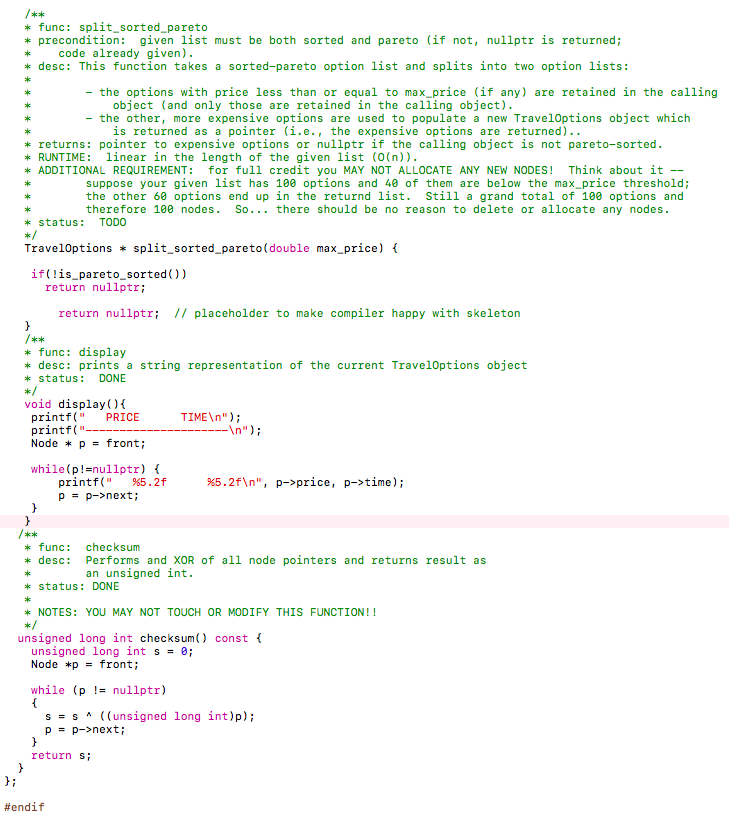
#lfndef #define _TRVL-OPTNS_A -TRVL-OPTNS_A #include #include #include price, a->time, b->price, b->time); public: sk k * func: push front * desc: Adds a Each pair is interpreted as a =0 ; i--) { options->push front (vec[i].first, veclil.second); return options; func: fromvec * desc: This function accepts a C++ standard 1libary vector of pair Each pair is interpreted as a -0 ; i--) { options->push front (vec[i].first, veclil.second); return options; func: to vec desc: Utility function which creates a C++ standard libary vector of pair and populates it with the options in the calling object (in the same order) As in from vec the "first" field of each pair maps to price and the "second" field maps to time returns: a pointer to the resulting vector k status DONE std: :vector> to_vec) const std:: vector> *vec std::vector>(); = new while(p nullptr) vec->push_back (std::pair (p->price, p->time)); p- p->next; return vec ak ak kst func: is_pareto sorted desc: returns true if and only if the list is: STRICTLY INCREASING IN price AND STRICTLY DECREASING IN time REQUIREMENTS: RUNTIME: linear in length of listn (i.e.,0(n)) * status TOD0 COMMENTS: notice that because of the runtime requirement, you cannot simply do this: return is-sorted ( ) && s-pareto(); x/ bool is pareto_sorted) const return false; ak * func : insertsorted *preconditions: given collection (calling object) must be sorted (but not necessarily - pareto). If this is not the case, false is returned (code provided) (returns true otherwise, after insertion complete) *desc: inserts option (given as parameters) into option list (calling object) while keeping it sorted. Recall: ordering by price; tie-breaker is time RUNTIME linear in length of list (n) * status: TODO ak NOTES/TIPS: do this before insert pareto_sorted; it is easier Remember, this one you don't have to think about pruning for this function just ordering. as bool insert sorted(double price, double time) if(!is_sorted()) return false return true: func: insert pareto_sorted preconditions given collection (calling object) must be sorted AND pareto (pruned) if this is not the case, false is returned (code segment for this test given) desc: (assuming the list is sorted and pareto): if the option given by the parameters price and time is NOT dominated by already existing options, the following results - new option is inserted maintaining the sorted property of the list, AND -any pre-existing options which are now suboptimal (i.e., dominated by the newly added option) are deleted If the new option is suboptimal, the list is simply unchanged In either case, true is returned (i.e., as long as the preconditions are met) RUNTIME REQUIREMENT: linear in the length of the list0 (n) REMEMBER: If the new option is useless (dominated by a pre-existing option), the list is unchanged (but you still return true if preconditions are met) You must maintain sorted order and don't forget to deallocate memory associated with any deleted nodes k status: TODO bool insert pareto sorted (double price, double time) if(!is_pareto sorted)) return falsei // your code here! return true sk k func: union_pareto sorted precondition: calling object and parameter collections must both be sorted and pareto (if not, nullptr is returned) desc: constructs "the sorted, pareto" union (as in set-union excluding dominated options) of the two collections and returns it as a newly created object RUNTIME: linear in the length of the two lists (suppose one list is of length n and the other is of length m, then the overall runtime must be 0 (n+m)) COMMENTS REMEMBER: after this operation, the collection must be both pareto and sorted TIPS: Think about what must be the FIRST option in the sorted union (bootstrap) - then think about what is the candidate for the 2nd option (if any) Remember a pareto-sorted list must be strictly increasing and price and strictly decreasing in time * status TODO TravelOptions union_pareto sorted (const TravelOptions &other)constf if lis pareto_sorted 1 lother.is pareto_sorted)) return nullptr return nullptr sk k func: prune sorted precondition: given collection must be sorted (if not, false is returned) desc: takes sorted list of options and removes dominated entries (and eliminates any duplicates) RUNTIME linear in the length of the list (0(n)) COMMENTS: the resulting list will be sorted AND pareto * status TODO bool prune sorted) if(!is sorted)) return false return true; sk k func: join plus plus preconditions none both the calling object and parameter are just Trave10ptions objects (not necessarily param: other a reference to another to a list of TravelOptions (thus, there are two option lists: the calling desc: suppose you are planning a trip composed of two "legs" sorted or pareto). object and the parameter) first you travel from city X to city Y (this is part of your plan - you need to stop in city Y) then you continue from city Y to city Z Let the calling object be the options for the X-to-Y leg and the parameter be the options for the Y-to-z leg Your job is to construct a pareto-sorted set of options for the entire trip and return the resulting Trave10ptions object as a pointer In principle, any option for the X-to-Y leg can be paird with any option for the Y-to-Z leg In such a pairing, the total price will be p1+p2 and the total time will be t1+t2, (i.e., option ) (This is why the operation is called join plus_plus) This function's job is to determine the sorted-pareto list of options for the entire trip and return it as a pointer to the object returns a pointer to a TravelOptions object capturing all non-dominated options for the entire trip from X-to-Z (i.e., even though the given lists may not be sorted or pareto, the resulting list will be both) status: TODO RUNTIME no runtime requirement TIPS: Start by thinking about the "cross-product" of the two option lists (i.e, enumerating all pairs) Leverage some of the other operations in this assignment insert pareto sorted might be especially useful! (probably ought to implement any functions you plan on using first!. Don't overthink this one there is no runtime requirement after all * BOUNDARY CONDITIONS: It Is possible that one of both of the given option lists is empty ! The result Is still we11-defined (also empty) An empty option list is NOT the same as a null pointer though a pointer to a new TravelOptions object -that object just happens to have an empty list you should still return Travel0ptions join plus plus (const TravelOptions &other) const f return nullptr; // placeholder to make the compiler happy func: join plus_max preconditions: both the calling object and the parameter are sorted-pareto lists (if not, nullptr is returned) desc: imagine a different scenario (vs. join plus_ plus) you are a parent with two children - one living in city A and the other living in city C and they are both coming home for the holidays (let's call your home C) You have a pareto-sorted option list for the A-to-C trip (this is the calling object) and a pareto-sorted option list for the B-to-C trip. Consider a particular option for the A-to-C trip and a particular option for the B-to-C trip Clearly, the total price for selecting these two options is p1+p2 However (unlike in the plus plus case), adding the t1 and t2 doesn't make sense right (the trips are in "parallel" What you care about as a parent is when BOTH of your children are home. This is determine by MAX(t1,t2). Thus, the resulting "composite" option in this case would be (hence the name join plus max). Your job is to construct the sorted-pareto "composite" option list capturing the options for getting both children home The resulting TravelOptions object is returned as a pointer (recall if the preconditions are not met, nullptr is returned RUNTIME: let N and M be the lengths of the respective lists given; your runtime must be linear in N+M (O(N+M)) * status TODO TIPS: This one will take some thought! If the specified runtime is possible, the resulting option list cannot be too large right (at most N+M in length)? But there NxM possible pairing of options. So enummerating all pairs of options cannot be an option (as was suggested for the _plus plus case). Start by figuring out what the FIRST (cheapest) option in the resulting list MUST be Remember that a sorted-pareto list must be strictly increasing in price and strictly decreasing in time Now think about what might be the 2nd option in the list you are building. It must cost more than the first AND take less time. To be more concrete, suppose your first option has total price of $100 and results in child A traveling for 12 hours and child B traveling for 8 hours. Does it make sense to spend more money on child B so they can get home in say 7 hours? Think about it The MAX function is important! TravelOptions join plus max (const Travel0ptions &other) const if!is_pareto) II !(other.is pareto))) return nullptr return nullptr; sk k func: sorted clone desc: returns a sorted Travel0ptions object which contains the same elements as the current object status DONE [but relies on to do item insert sorted] Travel0ptions *sorted clone) TravelOptions *sorted = new Trave10ptions(); Node *p = front; while(p nullptr) sorted->insert sorted(p->price, p->time) p = p->next; return sorted; func: split sorted pareto precondition: given list must be both sorted and pareto (if not, nullptr is returned; code already given) * desc: This function takes a sorted-pareto option list and splits into two option lists: - the options with price less than or equal to max_price (if any) are retained in the calling object (and only those are retained in the calling object) - the other, more expensive options are used to populate a new TravelOptions object whiclh is returned as a pointer i.e., the expensive options are returned) returns: pointer to expensive options or nullptr if the calling object is not pareto-sorted RUNTIME linear in the length of the given list (0 (n)) ADDITIONAL REQUIREMENT: for full credit you MAY NOT ALLOCATE ANY NEW NODES! Think about it - suppose your given list has 10e options and 40 of them are below the max_price threshold; the other 60 options end up in the returnd list. Still a grand total of 100 options and therefore 180 nodes. So... there should be no reason to delete or allocate any nodes. k status: TODO LOP Travel0ptions split sorted_pareto (double max price) if ( !is-pareto-sorted ( ) ) return nullptr return nullptr // placeholder to make compiler happy with skeleton func: display * desc: prints a string representation of the current Trave10ptions object k status DONE void display)( TIME "; printf(" PRICE printf( Node * p = front; while(p!=nullptr) { printf(" %5.2f p = p->next; %5.2f ", p->price, p->time); func: checksum desc: Performs and XOR of all node pointers and returns result as an unsigned int. k status: DONE NOTES: YOU MAY NOT TOUCH OR MODIFY THIS FUNCTION!! unsigned long int checksum) const unsigned long int s 8 Node *p - front; while (p !# nullptr) s = s ^ ((unsigned long int ) p); p- p->next; return s endif #lfndef #define _TRVL-OPTNS_A -TRVL-OPTNS_A #include #include #include price, a->time, b->price, b->time); public: sk k * func: push front * desc: Adds a Each pair is interpreted as a =0 ; i--) { options->push front (vec[i].first, veclil.second); return options; func: fromvec * desc: This function accepts a C++ standard 1libary vector of pair Each pair is interpreted as a -0 ; i--) { options->push front (vec[i].first, veclil.second); return options; func: to vec desc: Utility function which creates a C++ standard libary vector of pair and populates it with the options in the calling object (in the same order) As in from vec the "first" field of each pair maps to price and the "second" field maps to time returns: a pointer to the resulting vector k status DONE std: :vector> to_vec) const std:: vector> *vec std::vector>(); = new while(p nullptr) vec->push_back (std::pair (p->price, p->time)); p- p->next; return vec ak ak kst func: is_pareto sorted desc: returns true if and only if the list is: STRICTLY INCREASING IN price AND STRICTLY DECREASING IN time REQUIREMENTS: RUNTIME: linear in length of listn (i.e.,0(n)) * status TOD0 COMMENTS: notice that because of the runtime requirement, you cannot simply do this: return is-sorted ( ) && s-pareto(); x/ bool is pareto_sorted) const return false; ak * func : insertsorted *preconditions: given collection (calling object) must be sorted (but not necessarily - pareto). If this is not the case, false is returned (code provided) (returns true otherwise, after insertion complete) *desc: inserts option (given as parameters) into option list (calling object) while keeping it sorted. Recall: ordering by price; tie-breaker is time RUNTIME linear in length of list (n) * status: TODO ak NOTES/TIPS: do this before insert pareto_sorted; it is easier Remember, this one you don't have to think about pruning for this function just ordering. as bool insert sorted(double price, double time) if(!is_sorted()) return false return true: func: insert pareto_sorted preconditions given collection (calling object) must be sorted AND pareto (pruned) if this is not the case, false is returned (code segment for this test given) desc: (assuming the list is sorted and pareto): if the option given by the parameters price and time is NOT dominated by already existing options, the following results - new option is inserted maintaining the sorted property of the list, AND -any pre-existing options which are now suboptimal (i.e., dominated by the newly added option) are deleted If the new option is suboptimal, the list is simply unchanged In either case, true is returned (i.e., as long as the preconditions are met) RUNTIME REQUIREMENT: linear in the length of the list0 (n) REMEMBER: If the new option is useless (dominated by a pre-existing option), the list is unchanged (but you still return true if preconditions are met) You must maintain sorted order and don't forget to deallocate memory associated with any deleted nodes k status: TODO bool insert pareto sorted (double price, double time) if(!is_pareto sorted)) return falsei // your code here! return true sk k func: union_pareto sorted precondition: calling object and parameter collections must both be sorted and pareto (if not, nullptr is returned) desc: constructs "the sorted, pareto" union (as in set-union excluding dominated options) of the two collections and returns it as a newly created object RUNTIME: linear in the length of the two lists (suppose one list is of length n and the other is of length m, then the overall runtime must be 0 (n+m)) COMMENTS REMEMBER: after this operation, the collection must be both pareto and sorted TIPS: Think about what must be the FIRST option in the sorted union (bootstrap) - then think about what is the candidate for the 2nd option (if any) Remember a pareto-sorted list must be strictly increasing and price and strictly decreasing in time * status TODO TravelOptions union_pareto sorted (const TravelOptions &other)constf if lis pareto_sorted 1 lother.is pareto_sorted)) return nullptr return nullptr sk k func: prune sorted precondition: given collection must be sorted (if not, false is returned) desc: takes sorted list of options and removes dominated entries (and eliminates any duplicates) RUNTIME linear in the length of the list (0(n)) COMMENTS: the resulting list will be sorted AND pareto * status TODO bool prune sorted) if(!is sorted)) return false return true; sk k func: join plus plus preconditions none both the calling object and parameter are just Trave10ptions objects (not necessarily param: other a reference to another to a list of TravelOptions (thus, there are two option lists: the calling desc: suppose you are planning a trip composed of two "legs" sorted or pareto). object and the parameter) first you travel from city X to city Y (this is part of your plan - you need to stop in city Y) then you continue from city Y to city Z Let the calling object be the options for the X-to-Y leg and the parameter be the options for the Y-to-z leg Your job is to construct a pareto-sorted set of options for the entire trip and return the resulting Trave10ptions object as a pointer In principle, any option for the X-to-Y leg can be paird with any option for the Y-to-Z leg In such a pairing, the total price will be p1+p2 and the total time will be t1+t2, (i.e., option ) (This is why the operation is called join plus_plus) This function's job is to determine the sorted-pareto list of options for the entire trip and return it as a pointer to the object returns a pointer to a TravelOptions object capturing all non-dominated options for the entire trip from X-to-Z (i.e., even though the given lists may not be sorted or pareto, the resulting list will be both) status: TODO RUNTIME no runtime requirement TIPS: Start by thinking about the "cross-product" of the two option lists (i.e, enumerating all pairs) Leverage some of the other operations in this assignment insert pareto sorted might be especially useful! (probably ought to implement any functions you plan on using first!. Don't overthink this one there is no runtime requirement after all * BOUNDARY CONDITIONS: It Is possible that one of both of the given option lists is empty ! The result Is still we11-defined (also empty) An empty option list is NOT the same as a null pointer though a pointer to a new TravelOptions object -that object just happens to have an empty list you should still return Travel0ptions join plus plus (const TravelOptions &other) const f return nullptr; // placeholder to make the compiler happy func: join plus_max preconditions: both the calling object and the parameter are sorted-pareto lists (if not, nullptr is returned) desc: imagine a different scenario (vs. join plus_ plus) you are a parent with two children - one living in city A and the other living in city C and they are both coming home for the holidays (let's call your home C) You have a pareto-sorted option list for the A-to-C trip (this is the calling object) and a pareto-sorted option list for the B-to-C trip. Consider a particular option for the A-to-C trip and a particular option for the B-to-C trip Clearly, the total price for selecting these two options is p1+p2 However (unlike in the plus plus case), adding the t1 and t2 doesn't make sense right (the trips are in "parallel" What you care about as a parent is when BOTH of your children are home. This is determine by MAX(t1,t2). Thus, the resulting "composite" option in this case would be (hence the name join plus max). Your job is to construct the sorted-pareto "composite" option list capturing the options for getting both children home The resulting TravelOptions object is returned as a pointer (recall if the preconditions are not met, nullptr is returned RUNTIME: let N and M be the lengths of the respective lists given; your runtime must be linear in N+M (O(N+M)) * status TODO TIPS: This one will take some thought! If the specified runtime is possible, the resulting option list cannot be too large right (at most N+M in length)? But there NxM possible pairing of options. So enummerating all pairs of options cannot be an option (as was suggested for the _plus plus case). Start by figuring out what the FIRST (cheapest) option in the resulting list MUST be Remember that a sorted-pareto list must be strictly increasing in price and strictly decreasing in time Now think about what might be the 2nd option in the list you are building. It must cost more than the first AND take less time. To be more concrete, suppose your first option has total price of $100 and results in child A traveling for 12 hours and child B traveling for 8 hours. Does it make sense to spend more money on child B so they can get home in say 7 hours? Think about it The MAX function is important! TravelOptions join plus max (const Travel0ptions &other) const if!is_pareto) II !(other.is pareto))) return nullptr return nullptr; sk k func: sorted clone desc: returns a sorted Travel0ptions object which contains the same elements as the current object status DONE [but relies on to do item insert sorted] Travel0ptions *sorted clone) TravelOptions *sorted = new Trave10ptions(); Node *p = front; while(p nullptr) sorted->insert sorted(p->price, p->time) p = p->next; return sorted; func: split sorted pareto precondition: given list must be both sorted and pareto (if not, nullptr is returned; code already given) * desc: This function takes a sorted-pareto option list and splits into two option lists: - the options with price less than or equal to max_price (if any) are retained in the calling object (and only those are retained in the calling object) - the other, more expensive options are used to populate a new TravelOptions object whiclh is returned as a pointer i.e., the expensive options are returned) returns: pointer to expensive options or nullptr if the calling object is not pareto-sorted RUNTIME linear in the length of the given list (0 (n)) ADDITIONAL REQUIREMENT: for full credit you MAY NOT ALLOCATE ANY NEW NODES! Think about it - suppose your given list has 10e options and 40 of them are below the max_price threshold; the other 60 options end up in the returnd list. Still a grand total of 100 options and therefore 180 nodes. So... there should be no reason to delete or allocate any nodes. k status: TODO LOP Travel0ptions split sorted_pareto (double max price) if ( !is-pareto-sorted ( ) ) return nullptr return nullptr // placeholder to make compiler happy with skeleton func: display * desc: prints a string representation of the current Trave10ptions object k status DONE void display)( TIME "; printf(" PRICE printf( Node * p = front; while(p!=nullptr) { printf(" %5.2f p = p->next; %5.2f ", p->price, p->time); func: checksum desc: Performs and XOR of all node pointers and returns result as an unsigned int. k status: DONE NOTES: YOU MAY NOT TOUCH OR MODIFY THIS FUNCTION!! unsigned long int checksum) const unsigned long int s 8 Node *p - front; while (p !# nullptr) s = s ^ ((unsigned long int ) p); p- p->next; return s endif