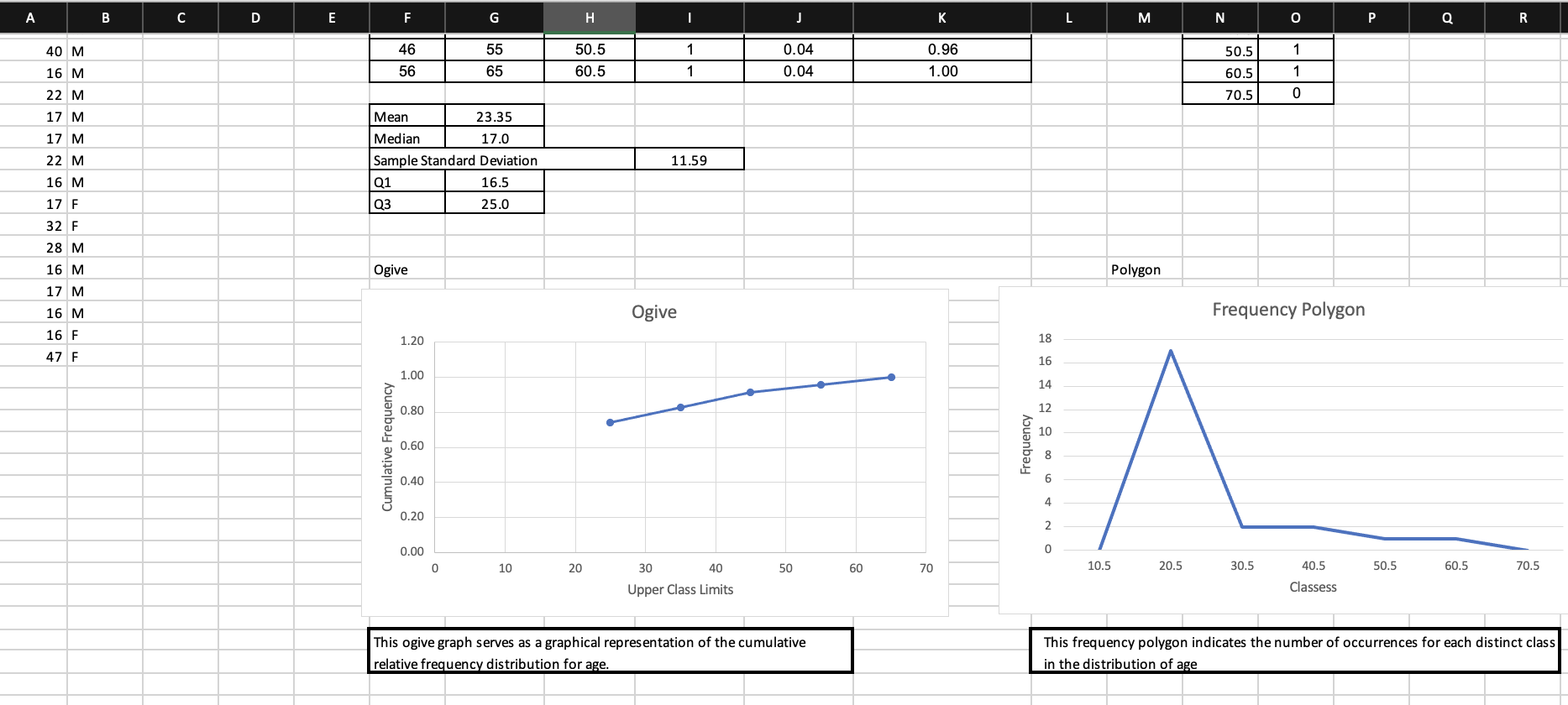
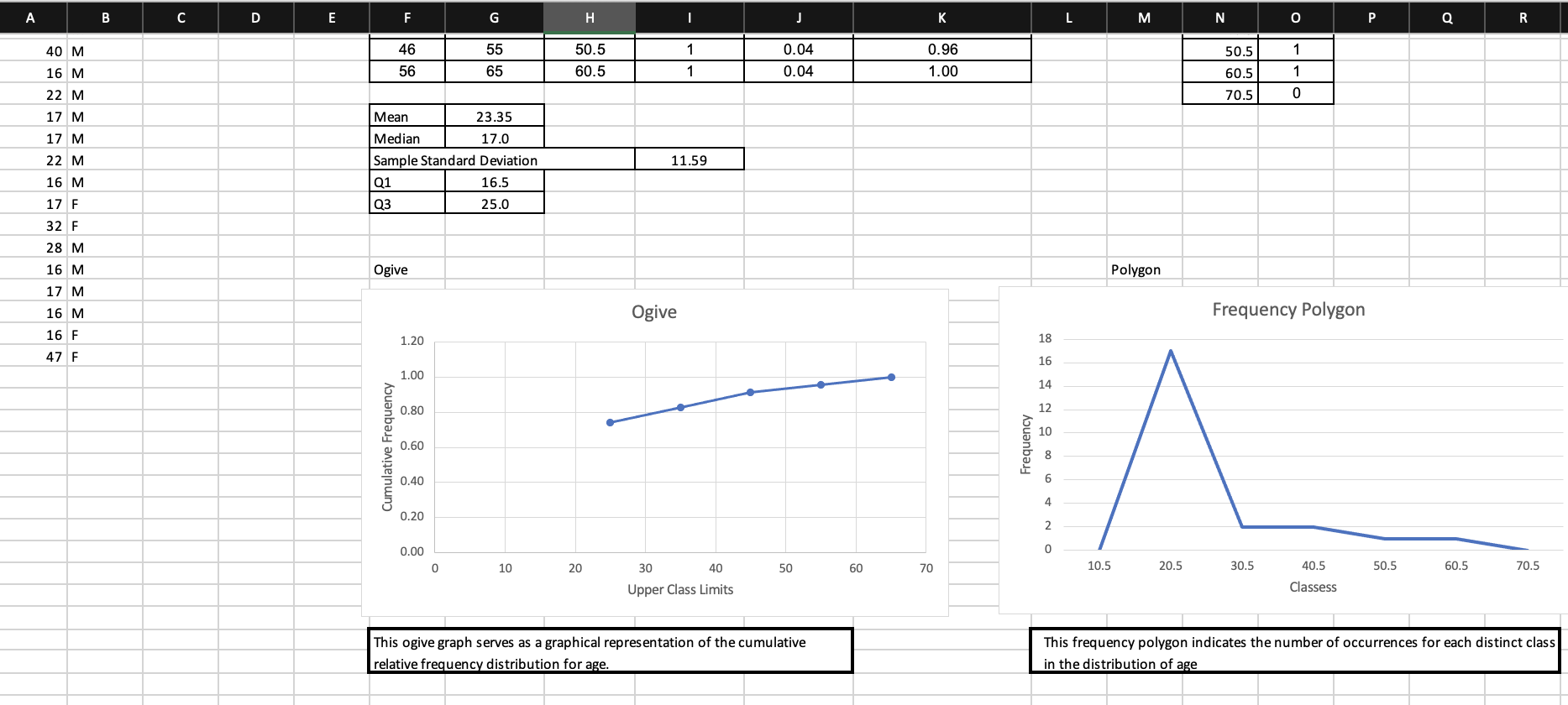
project: Part 3 - Confidence Intervals Assignment For this part of the project and based on the class sample, you will

create

a

95% confidence interval for the mean age and the proportion of males in the population of all online college students. Note: The goal of the project is to practice making a confidence interval for a mean and proportion with real data. Do not worry about failed assumptions tests and do not make corrections for small sample size. Use primary methods described in text and used on homework. Using the same excel sheet you submitted for Part 2, answer the following in the "Module 5" tab: ? For the average age, form a 95% confidence interval: o What distribution should be used? o What is the critical value? o What is the error bound? o What is the lower bound? o What is the upper bound? o How do we interpret the results, in context of our study? ? For the proportion of males, form a 95% confidence interval: o What distribution should be used? o What is the critical value? o What is the error bound? o What is the lower bound? o What is the upper bound? o How do we interpret the results, in context of our study?

Project: Part 4 - Hypothesis Tests Assignment For this part of the project and based on your sample, you will conduct a hypothesis test with ?= 0.05 to test two of the claims of the above article. Using the same excel sheet as Part 3, answer the following in the "Module 6" tab: ? Claim: the average age of online students is 32 years old. Can you prove it is not? o What is the null hypothesis? o What is the alternative hypothesis? o What distribution should be used? o What is the test statistic? o What is the p-value? o What is the conclusion? o How do we interpret the results, in context of our study? ? Claim: the proportion of males in online classes is 35%. Can you prove it is not? o What is the null hypothesis? o What is the alternative hypothesis? o What distribution should be used? o What is the test statistic? o What is the p-value? o What is the conclusion? o How do we interpret the results, in context of our study?

A B C D E F G H I K M N O P Q R 40 M 46 55 50.5 1 0.04 0.96 50.5 1 16 M 56 65 60.5 1 0.04 1.00 60.5 1 22 M 70.5 0 17 M Mean 23.35 17 M Median 17.0 22 M Sample Standard Deviation 11.59 16 M Q1 16.5 17 F 03 25.0 32 F 28 M 16 M Ogive Polygon 17 M 16 M Ogive Frequency Polygon 16 F 1.20 18 47 F 16 1.00 14 0.80 12 Frequency Cumulative Frequency 0.60 0.40 0.20 O 0.00 O 10 20 30 40 50 60 70 10.5 20.5 30.5 40.5 50.5 60.5 70.5 Upper Class Limits Classess This ogive graph serves as a graphical representation of the cumulative This frequency polygon indicates the number of occurrences for each distinct class relative frequency distribution for age. in the distribution of age