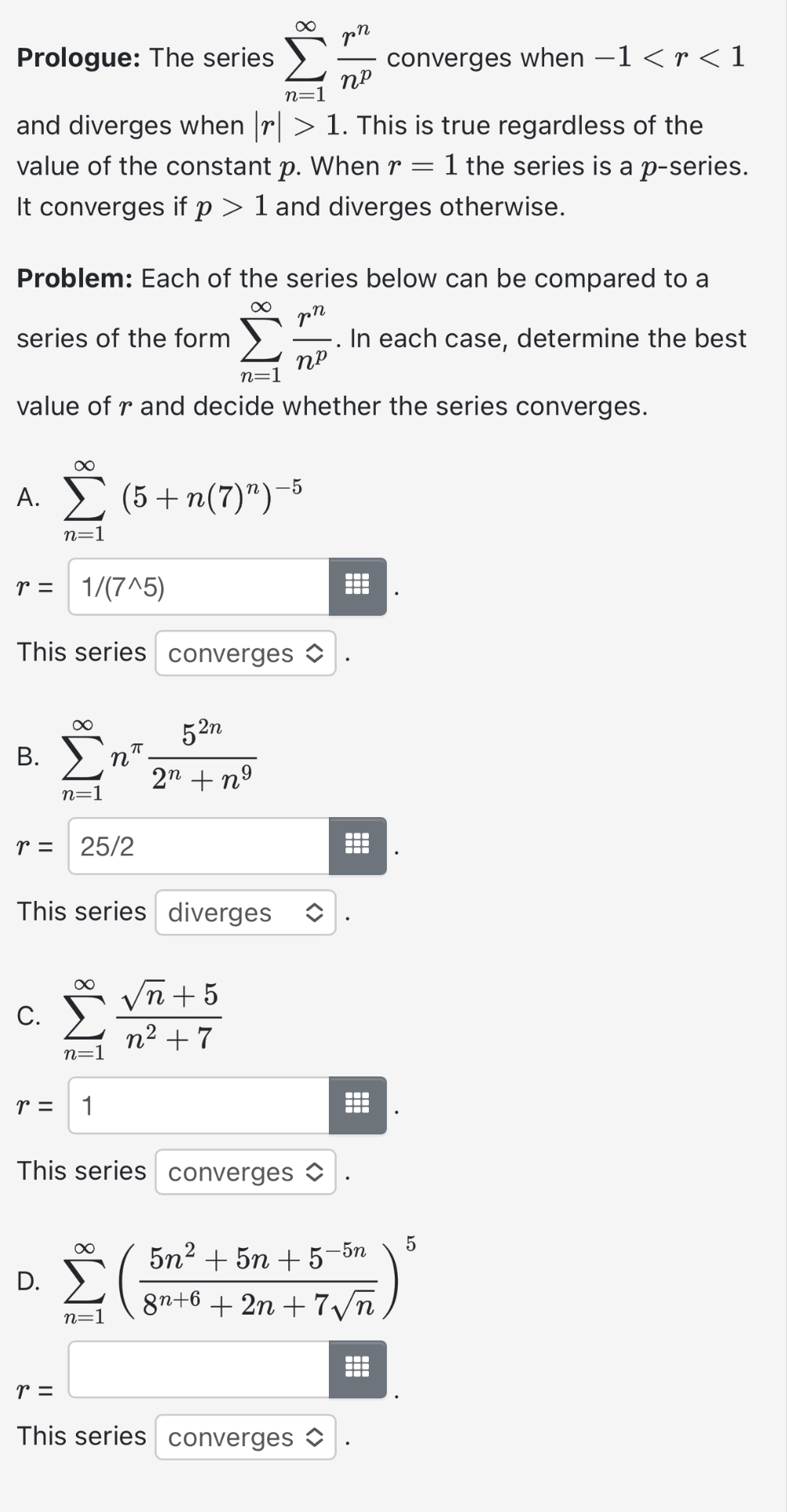
Prologue: The series converges when 1 < r < 1 n=] and diverges when |r| > 1. This is true regardless of the value of the constant p. When r = 1 the series is a p-series. It converges if p > 1 and diverges otherwise. Problem: Each of the series below can be compared to a series of the form In each case, determine the best np n=1 value of r and decide whether the series converges. A. (5+n(7)")-5 n=1 r = 1/(7^5) This series converges B. n=1 n" r = 25/2 52n 2n +ng This series diverges C. +5 n=1 n +7 r = 1 This series converges --- 5n2+5n+5-5 D. n=1 8n+6+2n+7n r = This series converges 5