Question: Prove that for fixed t the counting process N(t) has Poisson distribution with parameter at, i.e. N(t) Poisson(at) (Prove that the sum of two

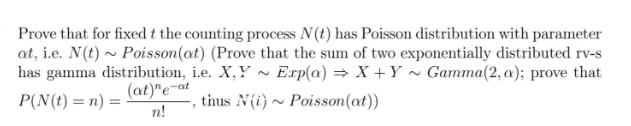
Prove that for fixed t the counting process N(t) has Poisson distribution with parameter at, i.e. N(t) Poisson(at) (Prove that the sum of two exponentially distributed rv-s has gamma distribution, i.e. X,Y Exp(a) X+Y~ Gamma(2, a); prove that 2 (at)ne-at P(N(t) = n) = Poisson(at)) n! T thus N(i)

Step by Step Solution

★★★★★

3.56 Rating (163 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To prove that the counting process Nt has a Poisson distribution with parameter at we need to show that PNt n ateat n The counting process Nt represen... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Accounting Questions!

Prove that if X has the t distribution with one degree of freedom, then 1/X also has the t distribution with one degree of freedom.

Prove that v = x + i y and v- = x - i y are linearly independent complex vectors if and only if their real and imaginary parts x and y are linearly independent real vectors.

Prove that if m + n and n + p are even integers, where m, n, and p are integers, then m + p is even. What kind of proof did you use?

Prove that the function (x, y) = 1/3 x 3 + 2/3 y 3/2 xy satisfies (x, y) 0 for x 0 and y 0. (a) First, verify that the set of critical points of f is the parabola y = x and that the Second...

Integrated Measurement Systems Inc. (IMS) is a Canadian public company that manufactures high-end measuring devices used primarily in the oil and natural gas industries. In 20X3, it had sales of $100...

The range R of a projectile propelled downward from the top of an inclined plane at an angle to the inclined plane is given by Where is the initial velocity of the projectile, is the angle the plane...

The following case was developed by the Ernst & Young Academic Resource Center, which is sponsored by the Ernest & Young Foundation. Robotic process automation is growing in importance in the...

Argue that for fixed $i$, the maximum in the optimal value function $W(i)=\max _{\mathbf{u}} W(i, \mathbf{u})$ among only all stationary policies must be assumed by some policy. Does your...

A management by objectives (MBO) approach relies on participative setting of objectives and using those objectives as the primary basis for assessing performance. The four-step process shown in...

=+37.9. Show that for T = [0,0) the coordinate-variable process [Z ,: t T] on (R, @) is not measurable.

In what type of situation would you need to create or replace a view? a . ) The view needs to have update, insert and delete statements allowed. b . ) One of the tables that the view references has...

Michelle Walker is the sole owner of Sandhill Vista Park, a public camping ground near the Crater Lake National Recreation Area. Michelle has compiled the following financial information as of...

The chart of accounts used by Notwist Copy Company is listed below. You are to indicate the proper accounts to be debited and credited for the following transactions. CHART OF ACCOUNTS Cash Accounts...

To influence the way in which managers make decisions within organisations, which of the following approaches should be adopted?" Performance measurement system. Reward structure. Performance...

Tutorial 10: Real Trigonometric Integrals Using a suitable contour integral, evaluate the following trigonometric integrals. 2T 2T 1. S cos 30 de 2. 5 - 4 cos 0 So 4 de 5+4 sin 0 2T 2T de de 4. 3. 2...

Personal Relationship O Criminal Intent Q.13. What type of Workplace Violence does this scenario match? Scenario: An Emergency Department patient kicks the attending doctor in the chest...

a. Find the current yield that existed on this bond at the beginning of the year. What was it by the end of the one-year holding period? b. Determine the holding period return on this investment....

In 1995 Miguel purchased a home for $130,000. In 2000 he sold it for $170,000 and immediately purchased another one for $180,000, which he sold in 2007 for $235,000. How much taxable capital gain, if...

In Example 6.8, we introduced the concept of a censored experiment in which n components are put on test and the experiment terminates as soon as r of the components have failed. Suppose component...

Refer to Exercise 1 and suppose the ten most recent values of the quality statistic are .0493, .0485, .0490, .0503, .0492, .0486, .0495, .0494, .0493, and .0488. Construct the relevant portion of the...

The water absorption of two types of mortar used to repair damaged cement was discussed in the article "Polymer Mortar Composite Matrices for Maintenance-Free, Highly Durable Ferrocement" (J. of...

In 2000, the Journal of the American Medical Association (JAMA) published a study that examined pregnancies that resulted in the birth of twins. Births were classified as preterm with intervention...

A company held a blood pressure screening clinic for its employees. The results are summarized in the table below by age group and blood pressure level: a) Find the marginal distribution of blood...

The Chance magazine article described in Exercise 15 further examined the impact of an applicant's ethnicity on the likelihood of admission to the Houston Independent School District's magnet schools...