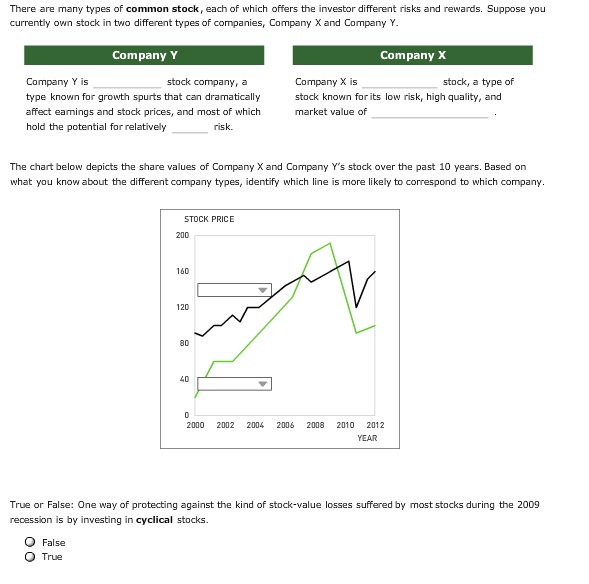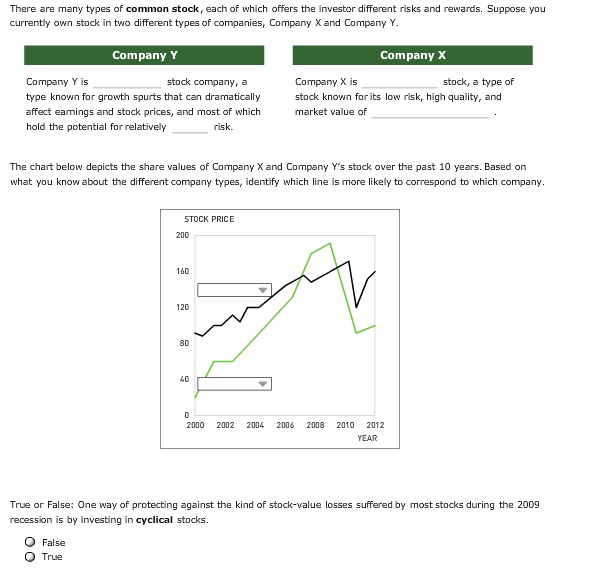
Provide solutions for the attached questions.
Simple linear regression is a statistical method that allows us to summarize and study relationships between two continuous (quantitative) variables: One variable, denoted X, is regarded as the predictor, explanatory, or independent variable. The other variable, denoted Y, is regarded as the response, outcome, or dependent variable. Suppose that we are given n-i.i.d observations { (x;, y;)}"_, from the assumed simple linear regression model Y = BIX + Bo + . Answer the following questions on simple linear regression. 5-a. Denote 1 and Bo as the point estimators of B, and Bo, respectively, that are obtained through the least squares method. Show, step by step, that the two point estimators are unbiased. Derive the least squares estimator of of and determine whether it is unbiased or not. Show your work step by step. 5-b. Calculate _'_1(yi - Bix; - Bo) (Bix, + Bo). Determine whether the point (X, Y) is on the line Y = 1X + Bo. Explain your reasoning mathematically. 5-c. Using the maximum likelihood estimation (MLE) technique, derive a point estimator for the coefficient B1 and the intercept Bo, respectively. Determine whether the point estimators that you obtained via MLE are unbiased or not. Justify your conclusion mathematically. 5-d. Calculate the variance of the four estimators from Questions 5-a and 5-c, respectively. Show your work step by step. 5-e. Suppose that we are using the simple linear regression model Y = B1 X + Bo + 1 while the true model is Y = 1X1 + B2X2 + Bo + 82 where Bo, B1, and B2 are constants. We assume that the distributions of &, and e2 are both N(0,02), i.e., normal distribution with variance o?. We further assume that the two noise variables are uncorrelated. Find the least squares estimator of B, in this case and determine whether the point estimator that you obtain is biased or not. If it is biased, calculate the bias.) Determine the inverse demand function. 0) Determine the vertical intercept of the inverse demand function. )Determine the horizontal intercept of the inverse demand function. d) Determine the slope of the inverse demand function. 2) Draw the consumer's inverse demand curve in Figure 1 provided in the answer booklet. Determine the market demand curve if there are 1000 consumers with the demand function Q = 40 - 5P 2) The demand functions for consumers 1, 2, and 3 are respectively Q1 = 60 - P, Q2 = 80 - 2P, and Q3 = 80 4P ) Determine the inverse demand function for each consumer. 0) Determine the vertical intercept for each inverse demand function. Determine the horizontal intercept for each inverse function. d) Determine the slope for each inverse demand function. 2) Determine the market demand curve. Draw the inverse market demand curve in Figure 2 provided in the answer booklet. 8) A consumer's demand function for good x is Qx = 8 - Px - Py/2 + 1/100 with Ox representing the quantity demand for good x, Px the price for good x, Py the price for good y, and I the consumer's income. ) Draw the inverse demand curve in Figure 3 provided in the answer booklet if Py = 2 and I = 100. 0) Draw the inverse demand curve in Figure 3 provided in the answer booklet if Py increases from 2 to 4 and I = 100. () Draw the inverse demand curve in Figure 3 provided in the answer booklet if I increases from 100 to 200 and Py = 2 1) A consumer's demand function for good x is @x = 50 - Px + 3Py/2 - Pz + 1/125 with Qx representing the quantity demand for good x, Px the price for good x, Py the price for good y, Pz the price for good z, and I the consumer's income.There are many types of common stock, each of which offers the investor different risks and rewards. Suppose you currently own stock in two different types of companies, Company X and Company Y. Company Y Company X Company Y is stock company, a Company X is stock, a type of type known for growth spurts that can dramatically stock known for its low risk, high quality, and affect earnings and stock prices, and most of which market value of hold the potential for relatively risk. The chart below depicts the share values of Company X and Company Y's stock over the past 10 years. Based on what you know about the different company types, identify which line is more likely to correspond to which company. STOCK PRICE 200 140 120 2000 2002 2004 2006 2008 2010 2012 YEAR True or False: One way of protecting against the kind of stock-value losses suffered by most stocks during the 2009 recession is by investing in cyclical stocks. False True