Answered step by step
Verified Expert Solution
Question
1 Approved Answer
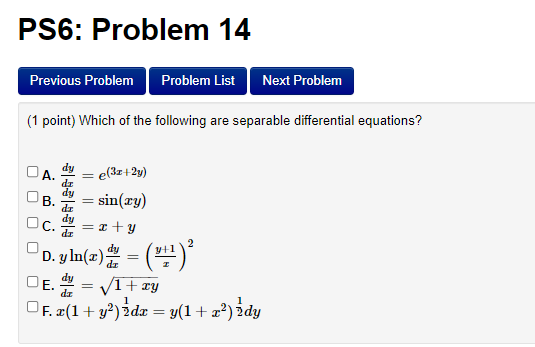
PS6: Problem 14 Previous Problem Problem List Next Problem (1 point) Which of the following are separable differential equations? DA. dy = (3:+2y) dy B.


Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


