Answered step by step
Verified Expert Solution
Question
1 Approved Answer
P-th percentile (0 < P 100) of a list of K ordered values (sorted from least to greatest) is the smallest value in the

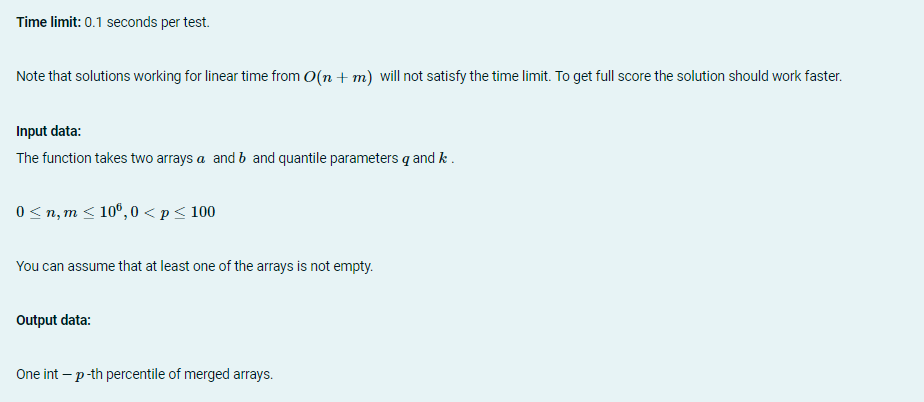
![Examples: # 1 2 3 4 a [1, 2, 7,8, 10] [1, 2, 7, 8] [15, 20, 35, 40, 50] [15, 20] b [6, 12] [6, 12] 0 [25, 40,](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/answers/2023/10/65213efadc753_62665213efa78ffd.jpg)

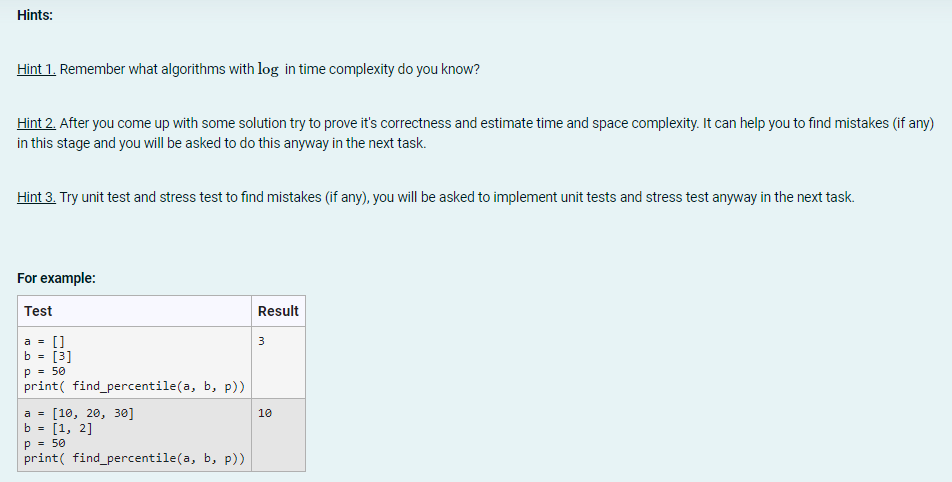
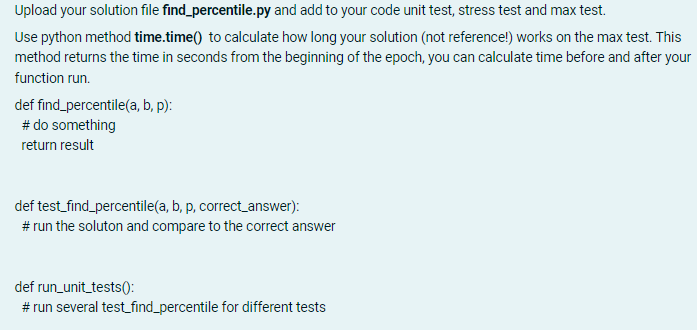

P-th percentile (0 < P 100) of a list of K ordered values (sorted from least to greatest) is the smallest value in the list such that no more than P percent of the data is strictly less than the value and at least P percent of the data is less than or equal to that value. It can be obtained by first calculating the ordinal rank and then taking the value from the ordered list that corresponds to that rank. The original rank k is calculated using this formula k = 100 K Given two sorted arraysa and b size of n and m. Implement a function find_percentile(a, b, p) that finds p-th percentile of an array c, where c is the result of merge arrays a and b. Time limit: 0.1 seconds per test. Note that solutions working for linear time from O(n + m) will not satisfy the time limit. To get full score the solution should work faster. Input data: The function takes two arraysa and b and quantile parameters q and k. 0 n, m 10,0 Examples: # 1 2 3 4 a [1, 2, 7, 8, 10] [1, 2, 7, 8] [15, 20, 35, 40, 50] [15, 20] b [6, 12] [6, 12] 0 [25, 40, 50] 50 50 30 40 output 7 6 20 20 Test sets: Part 1. 50-th percentile is called the median. For all tests from this test set p = 50 and you should find the median of two sorted arrays. For this test set n, m < 100 and solution working for linear time from n and m will satisfy the time limit. Part 2. For all tests p = 50,0 n, m 106. Solution working for O(n + m) will satisfy the time limit. Part 3. Small tests 0 n, m 100,0 < p 100. Part 4. Large tests 0 n, m 10,0 < p 100. Hints: Hint 1. Remember what algorithms with log in time complexity do you know? Hint 2. After you come up with some solution try to prove it's correctness and estimate time and space complexity. It can help you to find mistakes (if any) in this stage and you will be asked to do this anyway in the next task. Hint 3. Try unit test and stress test to find mistakes (if any), you will be asked to implement unit tests and stress test anyway in the next task. For example: Test a = [] b = [3] P = 50 print( find_percentile(a, b, p)) a = [10, 20, 30] b = [1, 2] P = 50 print( find_percentile(a, b, p)) Result 3 10 Upload your solution file find_percentile.py and add to your code unit test, stress test and max test. Use python method time.time() to calculate how long your solution (not reference!) works on the max test. This method returns the time in seconds from the beginning of the epoch, you can calculate time before and after your function run. def find percentile(a, b, p): # do something return result def test_find_percentile(a, b, p, correct_answer): # run the soluton and compare to the correct answer def run_unit_tests(): #run several test_find_percentile for different tests def run_stress_test(): #run several random tests #don't forget to find the right answer with refrence solution # find_percentile works 10 seconds on the max test def run_max_test() # generate arrays a and b of maximum possible sizes #len(a), len(b) P-th percentile (0 < P 100) of a list of K ordered values (sorted from least to greatest) is the smallest value in the list such that no more than P percent of the data is strictly less than the value and at least P percent of the data is less than or equal to that value. It can be obtained by first calculating the ordinal rank and then taking the value from the ordered list that corresponds to that rank. The original rank k is calculated using this formula k = 100 K Given two sorted arraysa and b size of n and m. Implement a function find_percentile(a, b, p) that finds p-th percentile of an array c, where c is the result of merge arrays a and b. Time limit: 0.1 seconds per test. Note that solutions working for linear time from O(n + m) will not satisfy the time limit. To get full score the solution should work faster. Input data: The function takes two arraysa and b and quantile parameters q and k. 0 n, m 10,0 Examples: # 1 2 3 4 a [1, 2, 7,8, 10] [1, 2, 7, 8] [15, 20, 35, 40, 50] [15, 20] b [6, 12] [6, 12] 0 [25, 40, 50] 50 50 30 40 output 7 6 20 20 Test sets: Part 1. 50-th percentile is called the median. For all tests from this test set p = 50 and you should find the median of two sorted arrays. For this test set n, m < 100 and solution working for linear time from n and m will satisfy the time limit. Part 2. For all tests p = 50,0 n, m 106. Solution working for O(n + m) will satisfy the time limit. Part 3. Small tests 0 n, m 100,0 < p 100. Part 4. Large tests 0 n, m 10,0 < p 100. Hints: Hint 1. Remember what algorithms with log in time complexity do you know? Hint 2. After you come up with some solution try to prove it's correctness and estimate time and space complexity. It can help you to find mistakes (if any) in this stage and you will be asked to do this anyway in the next task. Hint 3. Try unit test and stress test to find mistakes (if any), you will be asked to implement unit tests and stress test anyway in the next task. For example: Test a = [] b = [3] P = 50 print( find_percentile(a, b, p)) a = [10, 20, 30] b = [1, 2] P = 50 print( find_percentile(a, b, p)) Result 3 10 Upload your solution file find_percentile.py and add to your code unit test, stress test and max test. Use python method time.time() to calculate how long your solution (not reference!) works on the max test. This method returns the time in seconds from the beginning of the epoch, you can calculate time before and after your function run. def find_percentile(a, b, p): # do something return result def test_find_percentile(a, b, p, correct_answer): # run the soluton and compare to the correct answer def run_unit_tests(): #run several test_find_percentile for different tests def run_stress_test(): #run several random tests # don't forget to find the right answer with refrence solution # find_percentile works 10 seconds on the max test def run_max_test() # generate arrays a and b of maximum possible sizes #len(a), len(b)
Step by Step Solution
There are 3 Steps involved in it
Step: 1
The problem describes a task of finding the Pth percentile of the merged array resulting from two so...
Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


