[Python 3.7.2] Vapor Pressure Calculation using the Peng-Robinson Equation of State

Introduction

The purpose of this lab is to implement the calculation of vapor pressure of a pure liquid substance using a real-gas equation of state. The vapor pressure is the pressure at which a pure substance boils at a specific temperature (conversely, the boiling point temperature is the temperature at which a pure liquid substance boils at a specific pressure). We envision here a function whose inputs are (1) the identity of some pure substance (for example, water, benzene, hexane, ammonia, whatever), and (2) the temperature, and whose output is the vapor pressure of that substance at that temperature. Vapor-pressure calculations routinely performed as part of the design of chemical process units, such a distillation columns and flash separators.

The basis of this lab is the fact that vapor pressure is implicit in real-gas equations of state. Before we consider how our program to uncover vapor pressure will eventually work, let's first consider what we mean by real-gas equation of state. The ideal gas law

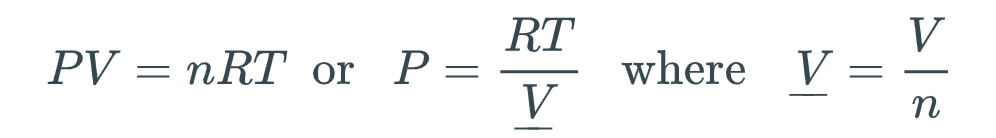
is an example of an equation of state, but it is not realistic enough to describe vapor-liquid equilibrium (e.g., boiling). The actual interrelationships among pressure, volume, moles, and temperature are much more complicated than the ideal gas law for real substances. One industry-standard "real-gas" equation of state is the Peng-Robinson (PR) equation.

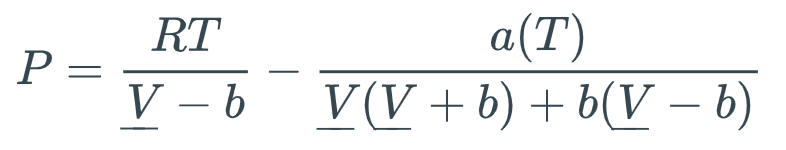
Here, b is a species-specific parameter representing volume-per-molecule and a(T) is a species-specific function of temperature representing intermolecular interactions. For most useful engineering calculations, the PR equation (and other real-gas equations of state -- everybody has their own favorite) is cast in the form of a cubic equation in the compressibility factor Z:

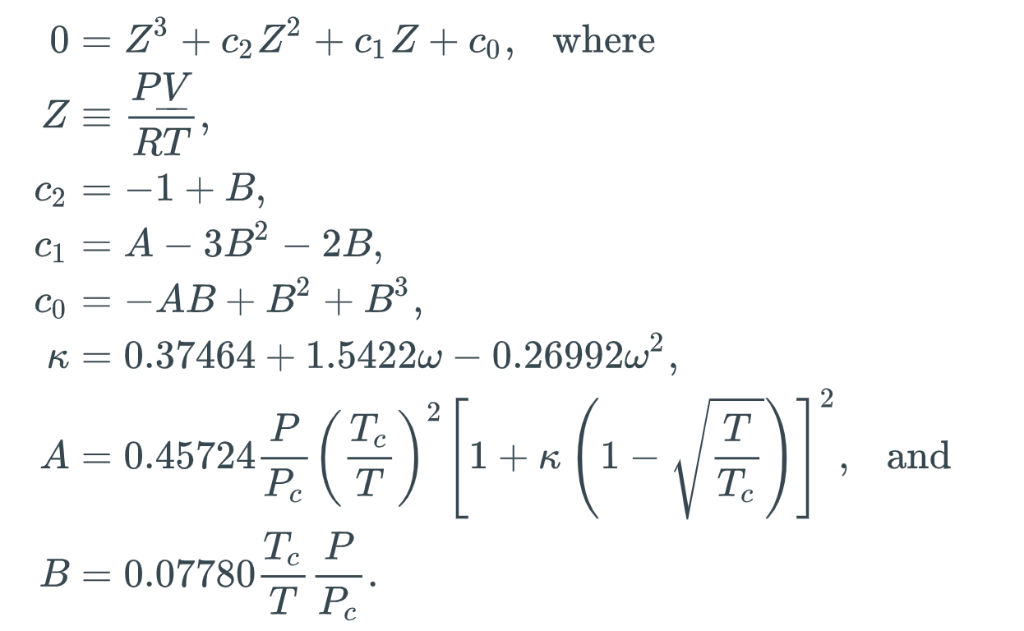
This may look complicated, but it really only has four parameters: the critical temperature T_c, the critical pressure P_c, the acentricity factor ("omega"), and the gas constant R. The temperature T and pressure P are considered variables, not parameters. In this cubic form, it is clear that the PR equation can have three roots. For certain values of the coefficients c₀, c₁, and c₂, there might exist three real roots, while for other values, there might exist only one real root (the other two are complex conjugates of each other). In the case that only one real root is found, there is only one phase (either liquid or vapor) at the specified T and P. However, in the case that three real roots are found, then the lowest one, say Z_L, is associated with a liquid, and the highest one, say Z_V, is associated with a vapor. (Here, the middle one is ignored.) Note that we use the following units: P [=] bar, T [=] K.

The existence of both a liquid root and a vapor root implies liquid-vapor coexistence, but it does not guarantee that P is the vapor pressure at T. To decide whether the liquid and vapor phases signified by the two roots of P-R are in fact in equilibrium with each other, one has to confirm that their fugacities are equal. Fugacity is a thermodynamic property derived by engineers to make phase-equilibrium calculations easy. For substances obeying the P-R equation of state, one can compute the fugacity f at a specific Z using this equation:

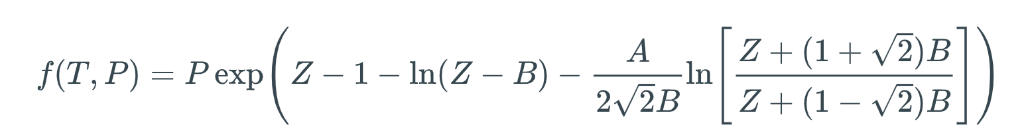
Here, the parameters A and B are the same ones used in PR above. So, if we are lucky enough to find real values for Z_L and Z_V at the requested T and our guess for P, we just plug them each into the fugacity equation independently to get two fugacity values; call them f_L and f_V, respectively. We then ask whether or not they have the same value. If so, then our guess P is P^vap(T). If not, we have to have an algorithm to adjust P until we get P^vap, signified by f_L = f_V.

The Algorithm

The convergent algorithm for computing P^vap at T using P-R is as follows:

1. Choose T_c, P_c, and for your substance;
2. Specify temperature T;
3. Guess a value for P (1 bar is good a lot of the time);
4. Compute the coefficients c₀, c₁, and c₂ using the equations for A and B that depend on T, P, T_c, P_c, and ;
5. Find the roots of the associated cubic using numpy.roots([1.0,c2,c1,c0]) (see below). The vapor-phase root Z_V is the first element returned by numpy.roots() (if it is real), and the liquid-phase root Z_L is the third element returned by numpy.roots() (if it is real).
6. If both Z_V and Z_L are real numbers (not complex), then compute the two fugacities using Eqn. 2: f_V=f(Z_V) and f_L=f(Z_L). If not, go to step 3. and choose a different initial guess for P (if Z is really small, use a lower guess; if Z is close to 1, use a higher guess).
7. If f_V and f_L are equal, then P is P^vap, and we're done. If not, adjust the value of P by multiplying it by f_L/f_V and go to step 4.

Using numpy.roots() to Find Roots of a Cubic

Part of your solution to this lab will require finding the roots of a cubic equation. The roots() function of the Numpy module makes this very easy. To use it, you should first import the NumPy module. (You may need to install on your own machine it first; don't worry -- the python in zyBooks has it already, and if you install Anaconda on your own laptop as recommended, you already have it.) Then, you can use the numpy.roots()function to find the root of any polynomial. roots() takes single array argument containing the coefficients of the polynomial, in a specific order. The first element is the coefficient on the highest power of x, the second is the coefficient on the second highest, and so forth. An array of n elements implies an n-1-order polynomial. Consider the interactive Python session below:

>>> from numpy import roots # return an array of -1, 1 as the roots to x^2 - 1 >>> roots([1,0,-1]) array([-1., 1.]) # compute roots of x^3 - 1 and store in array r >>> r = roots([1,0,0,-1]) >>> print(r[0]) (-0.5+0.866025403784j) >>> print(r[1]) (-0.5-0.866025403784j) >>> print(r[1].real) -0.5 >>> print(r[1].imag) -0.86602540784 >>> print(r[2]) (1+0j) # compute roots of x^3 - 6 x^2 + 11 x - 6 = (x-3)(x-2)(x-1); note order of elements in array r >>> r = roots([1,-6,11,-6]) >>> print(r[0]) 3. >>> print(r[1]) 2. >>> print(r[2]) 1.

Notice that the character j is Python's default for the imaginary number sqrt(-1), and complex numbers of tuples where the first element is the real part and the second is the imaginary part. One can access either part using the .real and .imag methods.

Assignment

Using an IDE or text editor on your own computer, download and edit the template main.py to completely implement the following four functions:

1. kappa(omega): Returns the value of given the value of
2. AB(T,P,Tc,Pc,omega): Returns both the values of PR parameters A and B given temperature T, pressure P, critical temperature T_c, critical pressure P_c, and acentricity factor .
3. pr_fug(z,A,B,P) : Computes the fugacity (in whatever units P has) given the value for Z(compressibility factor), A and B (the P-R parameters), and the pressure P (see eqn. 2).
4. Pvap(T,Pinit,Tc,Pc,omega,ep,maxiter) : Returns the vapor pressure P^vap at temperature T for the pure substance with critical constants T_c, P_c, and ; Pinit is an initial guess for the vapor pressure. ep is an optional argument with default value 1.e-6 that sets the tolerance for when two floating point numbers are "equal". maxiter is an optional argument with default value 1,000 that sets the maximum number of iterations in the above algorithm. Pvap() will call the functions pr_fug() and AB(), and AB() will call kappa().

Default Template:

def kappa ( omega ) : ''' your code here '''

def AB ( ''' argument(s) go here ''' ) : ''' your code here ''' def pr_fug ( ''' arguments(s) go here ''' ) : ''' your code here '''

def Pvap ( ''' arguments(s) go here ''' ) : crit = 0 numiter = 0 P = Pinit while abs(1.0-crit) > ep and numiter RT PV=nRT or P- where V- RT a(T) PV RT K 0.37464 + 1.54220-0.26992w2 A 0.45724 and T. P T PC B 0.07780 f(T, P) = P exp Z-1-ln(Z-B) RT PV=nRT or P- where V- RT a(T) PV RT K 0.37464 + 1.54220-0.26992w2 A 0.45724 and T. P T PC B 0.07780 f(T, P) = P exp Z-1-ln(Z-B)