Python coding question

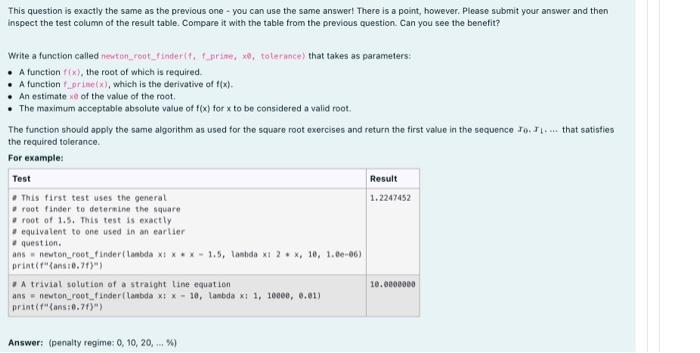
a The Newton-Raphson Method Be sure to watch the video introducing the Newton-Raphson method before proceeding We begin our exploration of numerical methods with a cool algorithm for finding the roots (zeros) of a function: the Newton-Raphson method, sometimes simply called Newton's method. Between 1665 and 1666, Isaac Newton (1642 - 1727) spent his days under lockdown in his countryside home at Woolsthorpe, England while the Great Plague was ravaging London. During these so-called "plague years" Newton was free to think, observe, and create. His many discoveries from this productive period of his life include the development of calculus, the laws of classical mechanics, the theory of gravitation, and the workings of optics. Among these massive achievements was a little algorithmic gem that we will now discuss. The algorithm The algorithm in question - which later became known simply as "Newton's Method" or the "Newton-Raphson Method" after Joseph Raphson (c. 1648 - c. 1715) who elaborated on the algorithm - could be used to find the roots of an arbitrary function. Finding a root of a function f() just means finding a value of such that t) = 0. Newton's method involves computing a series of increasing accurate estimates of the root as follows: 1. Choose an initial value for the root, 7, and call it to 2. Compute an improved estimate x142 11 - where f[?[?][?](x) is the derivative of f(x). 3. Go back to step 2 The above generates an intinite sequence of t; In practice we stop as soon as we have a sufficiently good" estimate of the actual root, as will be explained in the information panels and questions that follow. Lambda expressions So far in this course we have mostly defined functions using det statements. These take the general form: def function_namelparans): #Sone calculation return some_value_we_computed Python provides an alternative way to define simple functions that directly return a value easily computed from their parameters: lambda expressions. A lambda expression and don't be put off by the unfortunate name, which is of historical significance only) is an expression that evaluates to yield a function. A lambda expression takes the form Lambda parans: return_value_expression where parans is a comma separated list of parameters and return_value_expression is an expression that computes the return value from the parameters The following table should make this clearer. The left hand column shows a standard de statement to define a function. The right hand column shows how to achieve the same etfect using a lambda expression; the expression on the right-hand-side of the assignment statement yields a function and that function is assigned to a variable, thereby giving it a name. Using a dof statement Using a lambda expression det square square Labda xl xx return def plusia, b) returna. plus anda bi del quada, , , return a DXC dlanoda, b, c, x2 + + As we will see shortly, lambda expressions can be convenient as a way to pass very simple functions as parameters to functions like nesto root, oder to avoid the overhead of multiline det statements. Please see the lecture notes for an example using lambda expressions as the key argument when sorting lists This question is exactly the same as the previous one - you can use the same answer! There is a point, however. Please submit your answer and then inspect the test column of the result table. Compare it with the table from the previous question. Can you see the benefit? Write a function called neston_coot_tinderit, prime, xo, tolerance that takes as parameters: A function(x), the root of which is required. A function_orinet), which is the derivative of #lx). An estimate of the value of the root. The maximum acceptable absolute value of f(x) for x to be considered a valid root The function should apply the same algorithm as used for the square root oxercises and return the first value in the sequence to..... that satisties the required tolerance. For example: Test Result This first test uses the general 1.2247452 root finder to determine the square root of 1.5. This test is exactly # equivalent to one used in an earlier a question. ans newton_root_rinderlambda x** - 1.5, lambda x1 2 X, 10, 1.06-06) print("ans:8.713) A trivial solution of a straight line equation 10.0000000 ans = newton_root_funderlandda * * - 10, lambda x: 1, 10000, 0.01) print("ans:0.71)") Answer: (penalty regime: 0, 10, 20, ...)