Answered step by step
Verified Expert Solution
Question
1 Approved Answer
-python question -you may not import any other libraries or modules - i need help to modify my code in part D using the same
-python question 
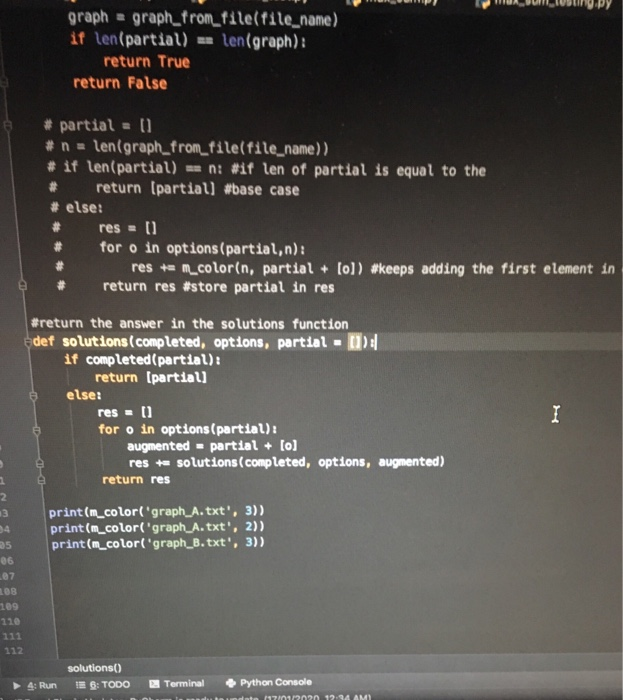
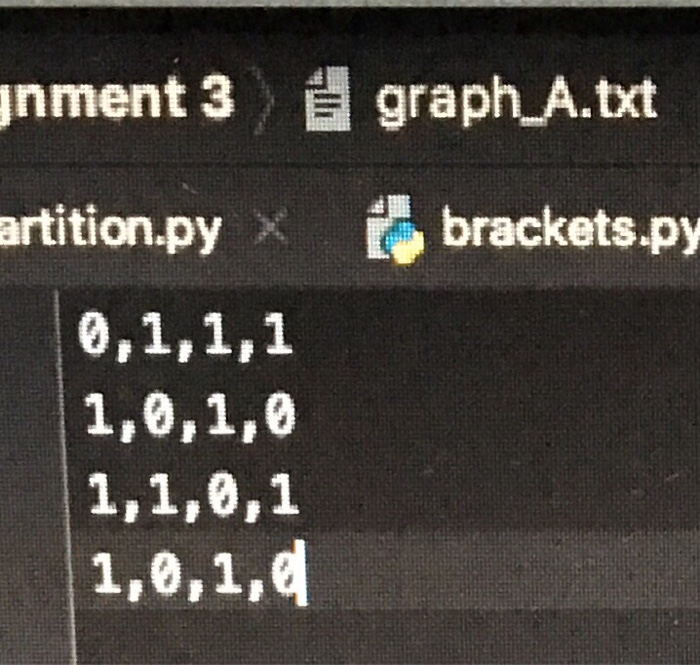
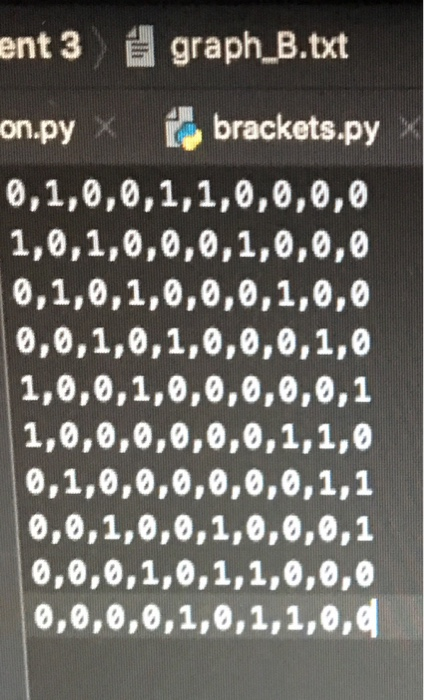
-you may not import any other libraries or modules
- i need help to modify my code in part D using the same functions
- all my codes from the previous parts are for referrence.








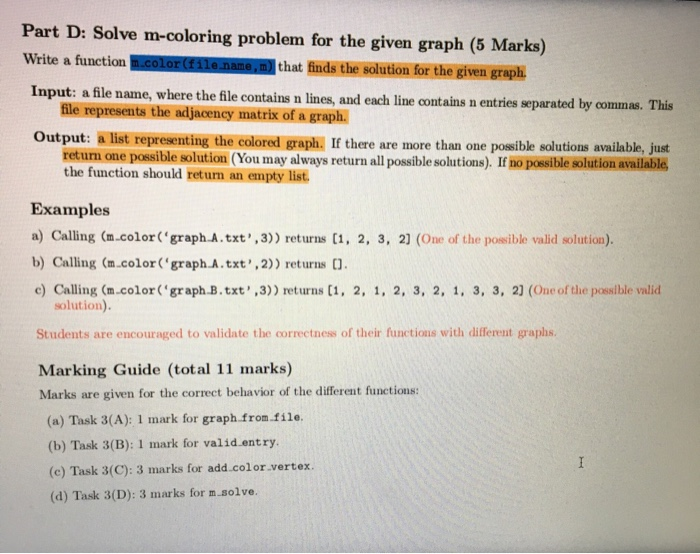
part A - gets the graph from text file by reading the file containing the graph.
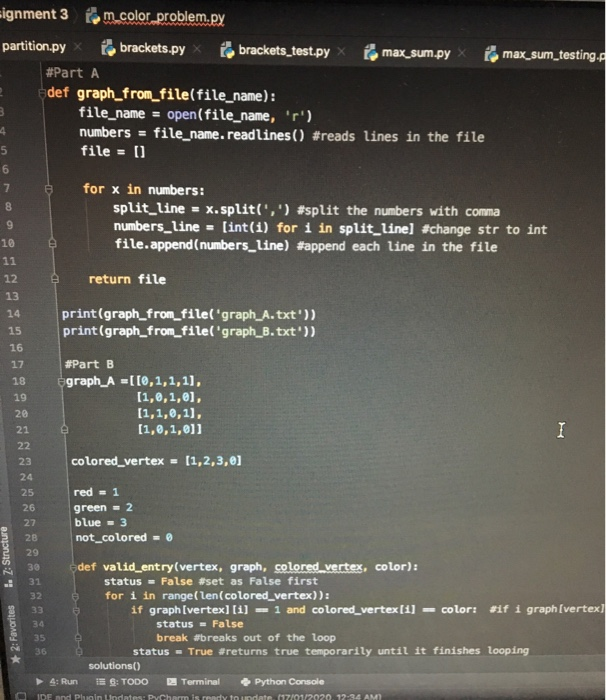
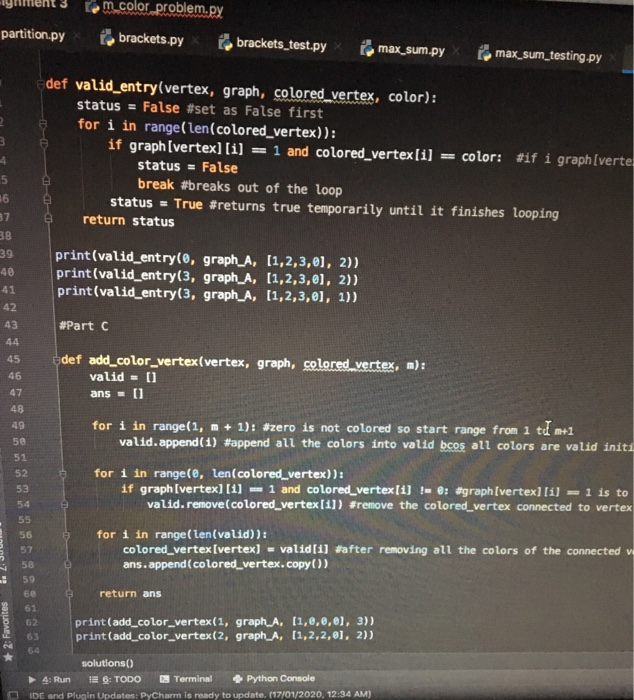
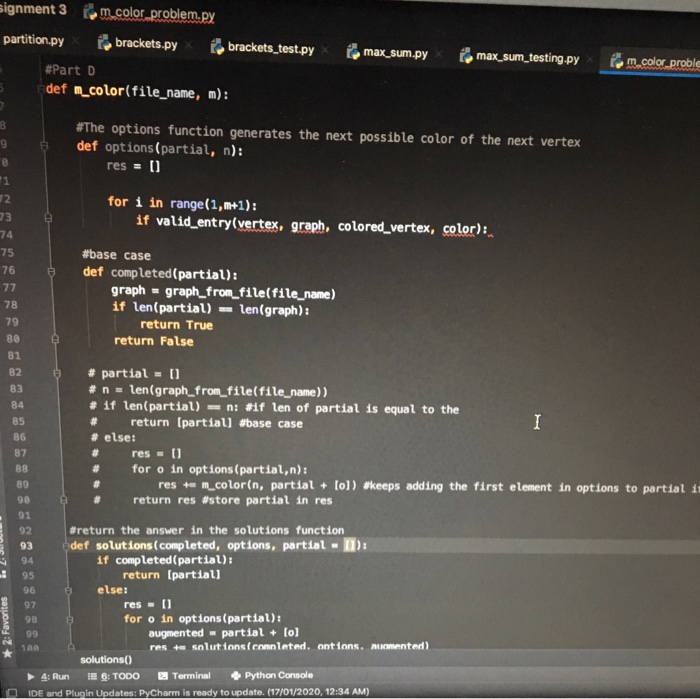
Task 4: m-Coloring problem (10 Marks) In this problem, an undirected graph is given. There is also provided m colors. The problem is to find if it is possible to assign nodes with m different colors, such that no two adjacent vertices of the graph are of the same colors. If the solution exists, the display which color is assigned on which wertex as shown in Figure 2. The graph coloring enjoys many practical applications as well as theoretical challenges. Some of the practical applications of graph coloring are pattern matching, scheduling, designing senting plans, exam timetalling. radio frequency assignment and solving Sudoku puzzles. Figure 2: An example of graph that can be colored with 3 different colors Create a Python module called .color problem.py. Within this module implement the following tasks Part A: Get graph from text file (1 Mark) Write a function graph.from.filefile name) that made in a file containing a raph and returns the contents of the file as a th a ble tale of Part D: Solve m-coloring problem for the given graph (5 Marks) Write a function .color (file name,m) that finds the solution for the given graph. Input: a file name, where the file contains n lines, and each line contains n entries separated by commas. This file represents the adjacency matrix of a graph. Output: a list representing the colored graph. If there are more than one possible solutions available, just retum one possible solution (You may always return all possible solutions). If no possible solution available the function should return an empty list. Examples a) Calling (m.color('graph.A.txt', 3)) returns (1, 2, 3, 2] (One of the possible valid solution). b) Calling (m.color('graph.A.txt', 2)) returns []. c) Calling (m.color('graph.B.txt',3)) returns (1, 2, 1, 2, 3, 2, 1, 3, 3, 2] (One of the possible valid solution). Students are encouraged to validate the correctness of their functions with different graphs. Marking Guide (total 11 marks) Marks are given for the correct behavior of the different functions: (a) Task 3(A): 1 mark for graph from file. (b) Task 3(B): 1 mark for valid entry. (e) Task 3(C): 3 marks for add.color vertex (d) Task 3(D): 3 marks for m.solve. signment 3 fom_color_problem.py partition.py _ brackets.py x brackets_test.py x max_sum.py x Pomax_sum_testing. #Part A def graph_from_file(file_name): file_name = open(file_name, 'r'). numbers = file_name, readlines() #reads lines in the file file = [] for x in numbers: split_line = x.split(',') #split the numbers with comma numbers_line - (int(1) for i in split_line] #change str to int file.append(numbers_line) #append each line in the file return file print(graph_from_filel'graph_A.txt')) print (graph_from_file('graph_B.txt')); #Part B egraph_A =[[0,1,1,1], (1,0,1,0), [1,1,,1), (1,0,1,0]] colored_vertex = (1,2,3,0) red = 1 green = 2 blue = 3 not_colored = ! 2: Structure * 2: Favorites def valid_entry(vertex, graph, colored vertex, color): status = False #set as False first for i in range(len(colored_vertex)): if graph [vertex][1] = 1 and colored_vertex [1] - color: #if i graph [vertex] status = False break #breaks out of the Loop status - True #returns true temporarily until it finishes looping solutions() 4: Run PE 6: TODO Terminal Python Console IDE and Plugin Undates: Pyhrn is rend toudate 21/2020. 12:34 AM Ignment 3 [om_color_problem.py partition.py brackets.py b rackets_test.py max_sum.py femax_sum_testing.py mino def valid_entry(vertex, graph, colored_vertex, color): status = False #set as False first for i in range( len(colored_vertex)): if graph (vertex][i] = 1 and colored_vertex [1] =color: #if i graph [verter status = False break #breaks out of the Loop status = True #returns true temporarily until it finishes looping return status print(valid_entry(@, graph_A, (1,2,3,0), 2)), print(valid_entry(3, graph_A, (1,2,3,0), 2)), print(valid_entry(3, graph_A, (1,2,3,0), 1)) #Part C def add_color_vertex(vertex, graph, colored_vertex, m): valid = [] ans = [] for i in range(1, m + 1): #zero is not colored so start range from 1 td ml valid.append(1) #append all the colors into valid bcos all colors are valid initi for i in range(e, len(colored_vertex)): if graph (vertex][1] - 1 and colored_vertex(1) I e: agraph (vertex][1] = 1 is to valid.remove(colored_vertex (11) Sremove the colored_vertex connected to vertex for i in range(len(valid)): colored_vertex [vertex) - valid(1) #after removing all the colors of the connected vi ans.append(colored_vertex.copy()) . .. return ans 2: Favorites print (add_color_vertex(1, graph A. (1,0,0,0), 3)) print(add_color_vertex(2, graph A. (1,2,2,0), 2)) 60 * solutions() 4: Run 1 : TODO_ Terminal Python Console IDE and Plugin Updates: PyCharm is ready to update. (17/01/2020, 12:34 AM) signment 3 Rom_color_problem.py partition.py brackets.py brackets_test.py #Part D def m_color(file_name, m): m ax_sum.py e max_sum_testing.py lem.color proble #The options function generates the next possible color of the next vertex def options(partial, n): res = 1) for i in range(1, m+1): if valid_entry(vertex, graph, colored_vertex, color), #base case def completed (partial): graph = graph_from_file(file_name) if len(partial) - len(graph): return True return false # partial = 0 # n - len(graph_from_file(file_name)) #if len(partial) = n *if len of partial is equal to the # return (partiall #base case # else: res = 0) for o in options(partial,n): rest m_colorin, partial. lol) #keeps adding the first element in options to partial in return res #store partial in res . 2.3 2: Favorites Wreturn the answer in the solutions function def solutions (completed, options, partial - if completed (partial): return (partiall else: res - 0 for o in options(partial): augmented - partial + [o] res + Solutions.comleted. ont ions. Aumented), solutions() 4: Run 6: TODO Terminal Python Console IDE and Plugin Updates: PyCharm is ready to update. (17/01/2020, 12:34 AM) O WAUMIVUNO.PY graph = graph_from_file(file_name) if len(partial) - len(graph): return True return false # partial = 0 # n = len(graph_from_file(file_name)) # if len(partial) - n #if len of partial is equal to the # return (partial] #base case # else: res = 11 for o in options(partial,n): res += m_colorin, partial + lo]) #keeps adding the first element in return res #store partial in res #return the answer in the solutions function Edet solutions (completed, options, partial (1) if completed (partial): return (partiall else: res = [] for o in options(partial): augmented - partial + lo] res te solutions(completed, options, augmented) return res dam print(m_color('graph_A.txt', 3)) print(m_color('graph_A.txt', 2)) print(m_color('graph_B.txt', 3)) 207 208 209 110 111 112 solutions() E 6: TODO 4: Run E Terminal Python Console 1 22.94 AM gnment 3 & graph_A.txt brackets.py artition.py 0,1,1,1 1,0,1,0 1,1,0,1 1,0,1,0 lent 3 graph_B.txt on.py brackets.py 0,1,0,0,1,1,0,0,0,0 1,0,1,0,0,0,1,0,0,0 0,1,0,1,0,0,0,1,0,0 0,0,1,0,1,0,0,0,1,0 1,0,0,1,0,0,0,0,0,1 1,0,0,0,0,0,0,1,1,0 0,1,0,0,0,0,0,0,1,1 0,0,1,0,0,1,0,0,0,1 0,0,0,1,0,1,1,0,0,0 0,0,0,0,1,0,1,1,0, Part B: Valid entry (1 Marks) Write a function valid entry(vertex.graph, colored vertex,color) that determines whether a particular color can be entered at a particular vertex in the graph, while maintaining validity. Input: vertex is an integer that represents the vertex that to be colored; graph is a nested list that repre- sents the adjacency matrix of the graph; colored vertex is a list that represents that the color of the vertices. For an example, a graph with 4 vertices, colored vertex can be represented by colored vertex -(1,2,3,0) (We may assume that red =1, green=2, blue - 3 and not colored -0. Assignment of colors are arbitrary, however, we assign not colored as 0). In this example, vertex O is colored by red, vertex 1 is colored as green, vertex 2 is colored as blue and vertex 3 is not colored; color is an integer represents the color to be added to vertex. Output: return a Boolean is the coloring is valid; otherwise False. Examples Given graph.A= [[0, 1, 1, 1) (1, 0, 1, 0] (1, 1, 0, 1). (1, 0, 1, 0]] a) Calling valid.entry(3.graph.A. (1,2,3,0).2) returns True. b) Calling valid entry(3.graph.A. (1,2,3,0),1) returns False. Part C: Assign colors to vertex (3 Marks) Write a function add.color.vertex(vertex,graph, colored vertex,n) that asins all the possible valid colors to a particular vertex Input: vertex is an integer that represents the vertex that to be colored: graph is a nested list that represents the adjacency matrix of the graph: colored vertex is a list that represents that the color of the vertices; a represents the number of the colors. Output: a neste list that represents all the possible valid color assignments to vertex. If no possible assignment of colors to the vertex available, then return an empty list. a) Calling add.color vertex (1. graph A. (1,0,0,0],3) returns ((1, 2, 0, 0), (1, 3, 0, 0]]. b) Calling add.color.vertex(2.graph A. (1, 2, 2, 0).2) returns 01. Task 4: m-Coloring problem (10 Marks) In this problem, an undirected graph is given. There is also provided m colors. The problem is to find if it is possible to assign nodes with m different colors, such that no two adjacent vertices of the graph are of the same colors. If the solution exists, the display which color is assigned on which wertex as shown in Figure 2. The graph coloring enjoys many practical applications as well as theoretical challenges. Some of the practical applications of graph coloring are pattern matching, scheduling, designing senting plans, exam timetalling. radio frequency assignment and solving Sudoku puzzles. Figure 2: An example of graph that can be colored with 3 different colors Create a Python module called .color problem.py. Within this module implement the following tasks Part A: Get graph from text file (1 Mark) Write a function graph.from.filefile name) that made in a file containing a raph and returns the contents of the file as a th a ble tale of Part D: Solve m-coloring problem for the given graph (5 Marks) Write a function .color (file name,m) that finds the solution for the given graph. Input: a file name, where the file contains n lines, and each line contains n entries separated by commas. This file represents the adjacency matrix of a graph. Output: a list representing the colored graph. If there are more than one possible solutions available, just retum one possible solution (You may always return all possible solutions). If no possible solution available the function should return an empty list. Examples a) Calling (m.color('graph.A.txt', 3)) returns (1, 2, 3, 2] (One of the possible valid solution). b) Calling (m.color('graph.A.txt', 2)) returns []. c) Calling (m.color('graph.B.txt',3)) returns (1, 2, 1, 2, 3, 2, 1, 3, 3, 2] (One of the possible valid solution). Students are encouraged to validate the correctness of their functions with different graphs. Marking Guide (total 11 marks) Marks are given for the correct behavior of the different functions: (a) Task 3(A): 1 mark for graph from file. (b) Task 3(B): 1 mark for valid entry. (e) Task 3(C): 3 marks for add.color vertex (d) Task 3(D): 3 marks for m.solve. signment 3 fom_color_problem.py partition.py _ brackets.py x brackets_test.py x max_sum.py x Pomax_sum_testing. #Part A def graph_from_file(file_name): file_name = open(file_name, 'r'). numbers = file_name, readlines() #reads lines in the file file = [] for x in numbers: split_line = x.split(',') #split the numbers with comma numbers_line - (int(1) for i in split_line] #change str to int file.append(numbers_line) #append each line in the file return file print(graph_from_filel'graph_A.txt')) print (graph_from_file('graph_B.txt')); #Part B egraph_A =[[0,1,1,1], (1,0,1,0), [1,1,,1), (1,0,1,0]] colored_vertex = (1,2,3,0) red = 1 green = 2 blue = 3 not_colored = ! 2: Structure * 2: Favorites def valid_entry(vertex, graph, colored vertex, color): status = False #set as False first for i in range(len(colored_vertex)): if graph [vertex][1] = 1 and colored_vertex [1] - color: #if i graph [vertex] status = False break #breaks out of the Loop status - True #returns true temporarily until it finishes looping solutions() 4: Run PE 6: TODO Terminal Python Console IDE and Plugin Undates: Pyhrn is rend toudate 21/2020. 12:34 AM Ignment 3 [om_color_problem.py partition.py brackets.py b rackets_test.py max_sum.py femax_sum_testing.py mino def valid_entry(vertex, graph, colored_vertex, color): status = False #set as False first for i in range( len(colored_vertex)): if graph (vertex][i] = 1 and colored_vertex [1] =color: #if i graph [verter status = False break #breaks out of the Loop status = True #returns true temporarily until it finishes looping return status print(valid_entry(@, graph_A, (1,2,3,0), 2)), print(valid_entry(3, graph_A, (1,2,3,0), 2)), print(valid_entry(3, graph_A, (1,2,3,0), 1)) #Part C def add_color_vertex(vertex, graph, colored_vertex, m): valid = [] ans = [] for i in range(1, m + 1): #zero is not colored so start range from 1 td ml valid.append(1) #append all the colors into valid bcos all colors are valid initi for i in range(e, len(colored_vertex)): if graph (vertex][1] - 1 and colored_vertex(1) I e: agraph (vertex][1] = 1 is to valid.remove(colored_vertex (11) Sremove the colored_vertex connected to vertex for i in range(len(valid)): colored_vertex [vertex) - valid(1) #after removing all the colors of the connected vi ans.append(colored_vertex.copy()) . .. return ans 2: Favorites print (add_color_vertex(1, graph A. (1,0,0,0), 3)) print(add_color_vertex(2, graph A. (1,2,2,0), 2)) 60 * solutions() 4: Run 1 : TODO_ Terminal Python Console IDE and Plugin Updates: PyCharm is ready to update. (17/01/2020, 12:34 AM) signment 3 Rom_color_problem.py partition.py brackets.py brackets_test.py #Part D def m_color(file_name, m): m ax_sum.py e max_sum_testing.py lem.color proble #The options function generates the next possible color of the next vertex def options(partial, n): res = 1) for i in range(1, m+1): if valid_entry(vertex, graph, colored_vertex, color), #base case def completed (partial): graph = graph_from_file(file_name) if len(partial) - len(graph): return True return false # partial = 0 # n - len(graph_from_file(file_name)) #if len(partial) = n *if len of partial is equal to the # return (partiall #base case # else: res = 0) for o in options(partial,n): rest m_colorin, partial. lol) #keeps adding the first element in options to partial in return res #store partial in res . 2.3 2: Favorites Wreturn the answer in the solutions function def solutions (completed, options, partial - if completed (partial): return (partiall else: res - 0 for o in options(partial): augmented - partial + [o] res + Solutions.comleted. ont ions. Aumented), solutions() 4: Run 6: TODO Terminal Python Console IDE and Plugin Updates: PyCharm is ready to update. (17/01/2020, 12:34 AM) O WAUMIVUNO.PY graph = graph_from_file(file_name) if len(partial) - len(graph): return True return false # partial = 0 # n = len(graph_from_file(file_name)) # if len(partial) - n #if len of partial is equal to the # return (partial] #base case # else: res = 11 for o in options(partial,n): res += m_colorin, partial + lo]) #keeps adding the first element in return res #store partial in res #return the answer in the solutions function Edet solutions (completed, options, partial (1) if completed (partial): return (partiall else: res = [] for o in options(partial): augmented - partial + lo] res te solutions(completed, options, augmented) return res dam print(m_color('graph_A.txt', 3)) print(m_color('graph_A.txt', 2)) print(m_color('graph_B.txt', 3)) 207 208 209 110 111 112 solutions() E 6: TODO 4: Run E Terminal Python Console 1 22.94 AM gnment 3 & graph_A.txt brackets.py artition.py 0,1,1,1 1,0,1,0 1,1,0,1 1,0,1,0 lent 3 graph_B.txt on.py brackets.py 0,1,0,0,1,1,0,0,0,0 1,0,1,0,0,0,1,0,0,0 0,1,0,1,0,0,0,1,0,0 0,0,1,0,1,0,0,0,1,0 1,0,0,1,0,0,0,0,0,1 1,0,0,0,0,0,0,1,1,0 0,1,0,0,0,0,0,0,1,1 0,0,1,0,0,1,0,0,0,1 0,0,0,1,0,1,1,0,0,0 0,0,0,0,1,0,1,1,0, Part B: Valid entry (1 Marks) Write a function valid entry(vertex.graph, colored vertex,color) that determines whether a particular color can be entered at a particular vertex in the graph, while maintaining validity. Input: vertex is an integer that represents the vertex that to be colored; graph is a nested list that repre- sents the adjacency matrix of the graph; colored vertex is a list that represents that the color of the vertices. For an example, a graph with 4 vertices, colored vertex can be represented by colored vertex -(1,2,3,0) (We may assume that red =1, green=2, blue - 3 and not colored -0. Assignment of colors are arbitrary, however, we assign not colored as 0). In this example, vertex O is colored by red, vertex 1 is colored as green, vertex 2 is colored as blue and vertex 3 is not colored; color is an integer represents the color to be added to vertex. Output: return a Boolean is the coloring is valid; otherwise False. Examples Given graph.A= [[0, 1, 1, 1) (1, 0, 1, 0] (1, 1, 0, 1). (1, 0, 1, 0]] a) Calling valid.entry(3.graph.A. (1,2,3,0).2) returns True. b) Calling valid entry(3.graph.A. (1,2,3,0),1) returns False. Part C: Assign colors to vertex (3 Marks) Write a function add.color.vertex(vertex,graph, colored vertex,n) that asins all the possible valid colors to a particular vertex Input: vertex is an integer that represents the vertex that to be colored: graph is a nested list that represents the adjacency matrix of the graph: colored vertex is a list that represents that the color of the vertices; a represents the number of the colors. Output: a neste list that represents all the possible valid color assignments to vertex. If no possible assignment of colors to the vertex available, then return an empty list. a) Calling add.color vertex (1. graph A. (1,0,0,0],3) returns ((1, 2, 0, 0), (1, 3, 0, 0]]. b) Calling add.color.vertex(2.graph A. (1, 2, 2, 0).2) returns 01 part B - detremines whether a partiular color can be entered at a particular vertex at the graph
part C - assigns all the particular valid colors to a particular vertex
part D - finds the solution for the given graph 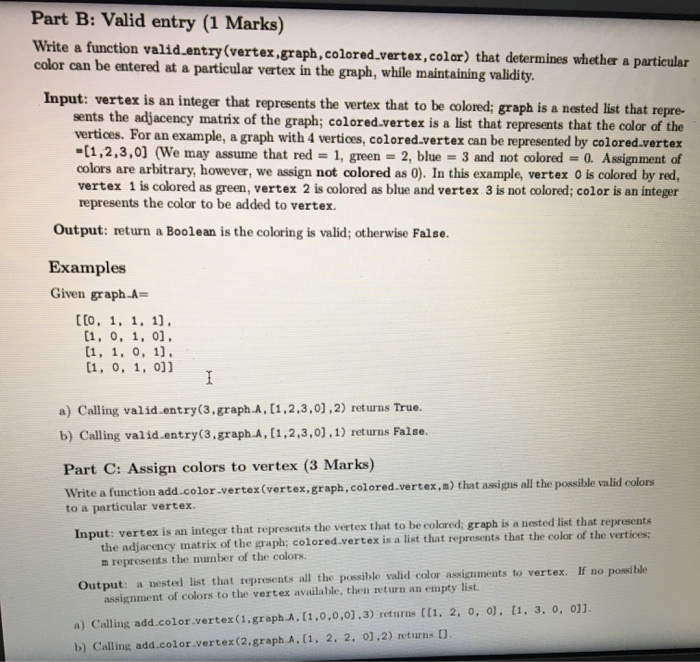

Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


