PYTHON


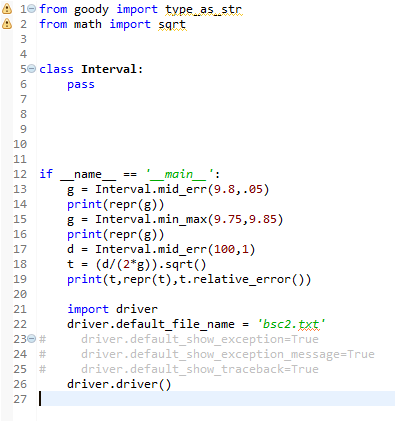
Write a class that represents and defines operators for Interval numbers, which are represented by a pair numeric values: int, float or mixed. We use intervals to represent approximate numbers, whose exact value we do not know. For example, in physics we might know that the acceleration produced by the the force of gravity (g) at sea level is 9.8 m/s2 +/- .05 m/s2, which we will writ a9.8(+-.05) m/s2. With this class we can perform numeric calculations on Interval objects, which automatically keep track of the precision for each calculated value For example, the formula sqrt(d/(2*g)) computes the amount of time it takes for an object at sea level to fall a given distance (d) in a vacuum. Given our approximation for g, and a distance that is 100(+/-1) m, we can use the Interval class to compute the amount of time it takes for an object to drop this amount as follows, including the precision with which we know the answer g Interval.mid..err(9.8,.05) d Interval.mid.err(100, 1) t = (d/(2"g)).sqrt() print(t) So, with g known +.05 m/s, and d known +/-1 m, the results print as 2.2587923826805945(+/-0.017056289680373204)). which indicates that the time will be somewhere between about 2.24 and 2.28 seconds, having a relative error of about 7.6%. Note that each Interval object will store the minimum and maximum value in the interval. So 9.8(+/-.05) is stored as an Interval with a minimum of 9.75 and a maximum of 9.85 Details 1. Define a class named Interval in a module named interval.py 2. Define an init method that has two parameters; their arguments specify the minimum and maximum values in the interval respectively. Store them in the self variables min and max. Programmers will not use this method directly to construct Interval objects; instead, they will use the static Interval.min_max and Intervalmid err methods (described below) For information about static methods, read the Class Review lecture notes (look for the entry on Static Methods near the bottom, before the problems) 3. Define a static min max method that has two parameters; their arguments specify the minimum and maximum values in the interval. The second parameter is optional, with None as its default value. This method should raise an AssertionError exception, with an appropriate message, if (a) the first argument is not an int or float numeric type or (b) if the second argument is not a numeric type or None, or (c) the first argument is greater than the second; if the second argument is None, use the first argument for both the minimum and maximum value (creating an interval with one value representing exactly that number). Return the appropriate Interval object. 4. Define a static mid err method that has two parameters; their arguments specify the middle value and the +/- error for the interval. The second parameter is optional, with 0 as its default value. This method should raise an AssertionError exception, with an approprate message, if (a) the first argument is not an int or float numeric type, or (b) if the second argument is not a numeric type, or (c) if the second argument is negative. Return the appropriate Interval object. For example, Intervalmid err(9.8,.05). would produce the same object as Intervalmin max(9.75,9.85) 5. Define the methods best, error, and relative_error o best returns the best approximation for the Interval (the value at its middle) o error returns the error for the Interval: half the distance between its minimum and maximum values o relative error returns the absolute value of the ratio between the error over the best approximation as a percentage (multiply by 100) Write a class that represents and defines operators for Interval numbers, which are represented by a pair numeric values: int, float or mixed. We use intervals to represent approximate numbers, whose exact value we do not know. For example, in physics we might know that the acceleration produced by the the force of gravity (g) at sea level is 9.8 m/s2 +/- .05 m/s2, which we will writ a9.8(+-.05) m/s2. With this class we can perform numeric calculations on Interval objects, which automatically keep track of the precision for each calculated value For example, the formula sqrt(d/(2*g)) computes the amount of time it takes for an object at sea level to fall a given distance (d) in a vacuum. Given our approximation for g, and a distance that is 100(+/-1) m, we can use the Interval class to compute the amount of time it takes for an object to drop this amount as follows, including the precision with which we know the answer g Interval.mid..err(9.8,.05) d Interval.mid.err(100, 1) t = (d/(2"g)).sqrt() print(t) So, with g known +.05 m/s, and d known +/-1 m, the results print as 2.2587923826805945(+/-0.017056289680373204)). which indicates that the time will be somewhere between about 2.24 and 2.28 seconds, having a relative error of about 7.6%. Note that each Interval object will store the minimum and maximum value in the interval. So 9.8(+/-.05) is stored as an Interval with a minimum of 9.75 and a maximum of 9.85 Details 1. Define a class named Interval in a module named interval.py 2. Define an init method that has two parameters; their arguments specify the minimum and maximum values in the interval respectively. Store them in the self variables min and max. Programmers will not use this method directly to construct Interval objects; instead, they will use the static Interval.min_max and Intervalmid err methods (described below) For information about static methods, read the Class Review lecture notes (look for the entry on Static Methods near the bottom, before the problems) 3. Define a static min max method that has two parameters; their arguments specify the minimum and maximum values in the interval. The second parameter is optional, with None as its default value. This method should raise an AssertionError exception, with an appropriate message, if (a) the first argument is not an int or float numeric type or (b) if the second argument is not a numeric type or None, or (c) the first argument is greater than the second; if the second argument is None, use the first argument for both the minimum and maximum value (creating an interval with one value representing exactly that number). Return the appropriate Interval object. 4. Define a static mid err method that has two parameters; their arguments specify the middle value and the +/- error for the interval. The second parameter is optional, with 0 as its default value. This method should raise an AssertionError exception, with an approprate message, if (a) the first argument is not an int or float numeric type, or (b) if the second argument is not a numeric type, or (c) if the second argument is negative. Return the appropriate Interval object. For example, Intervalmid err(9.8,.05). would produce the same object as Intervalmin max(9.75,9.85) 5. Define the methods best, error, and relative_error o best returns the best approximation for the Interval (the value at its middle) o error returns the error for the Interval: half the distance between its minimum and maximum values o relative error returns the absolute value of the ratio between the error over the best approximation as a percentage (multiply by 100)









