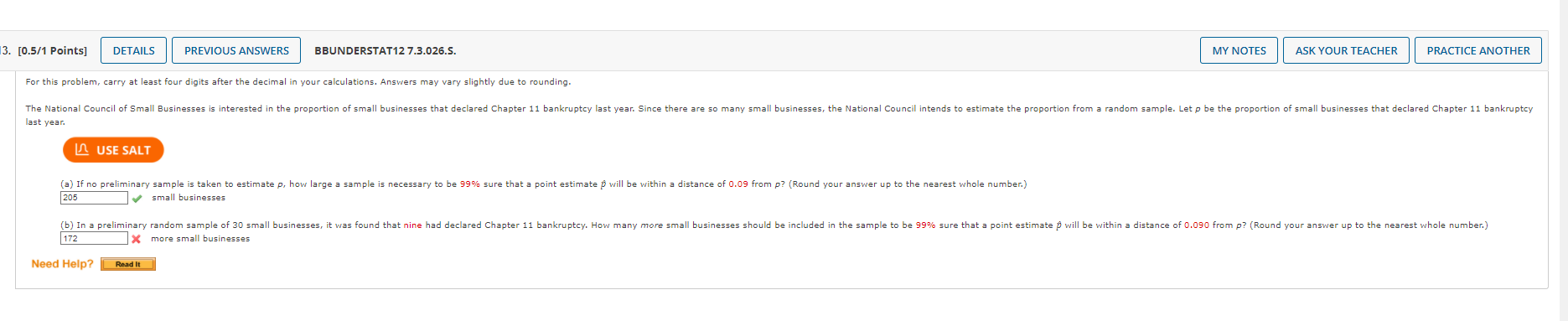
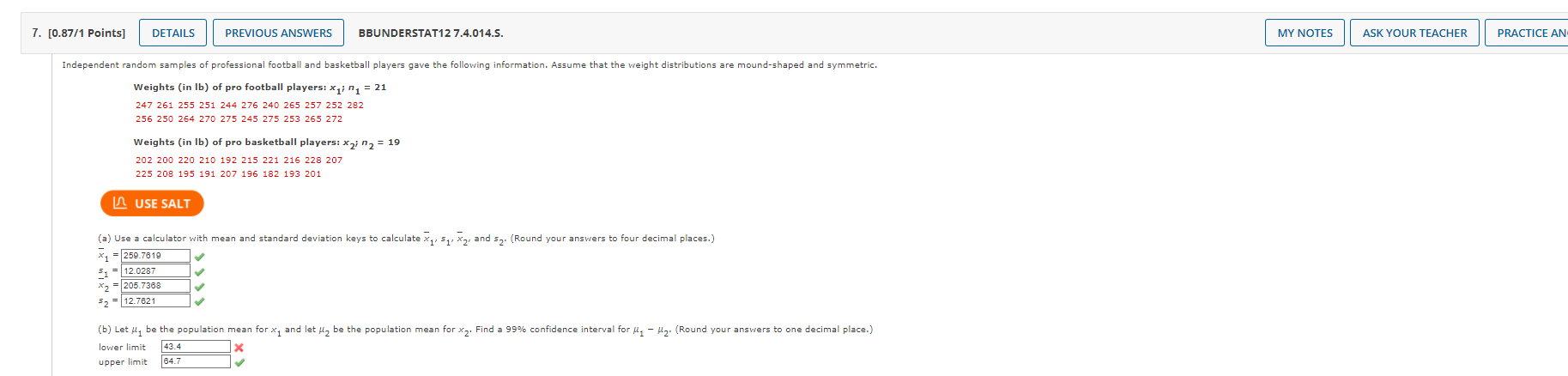
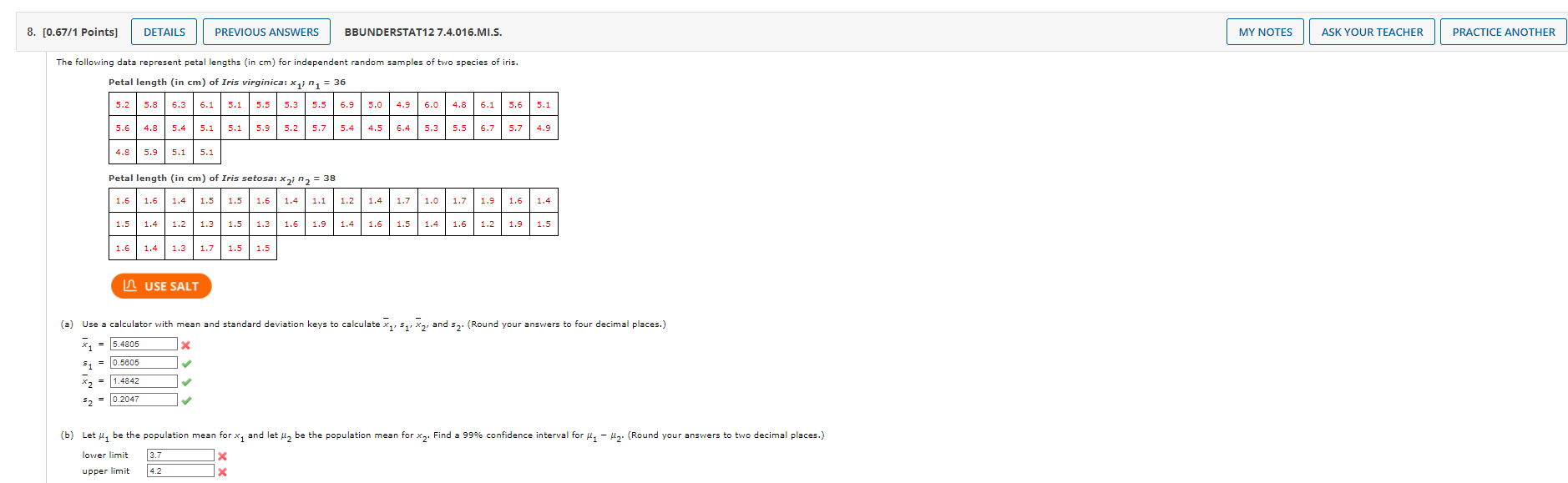
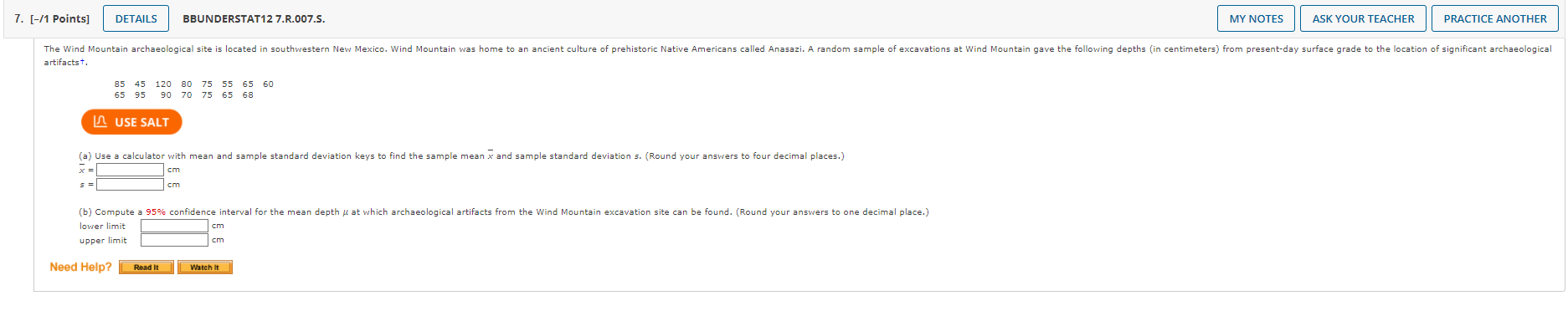
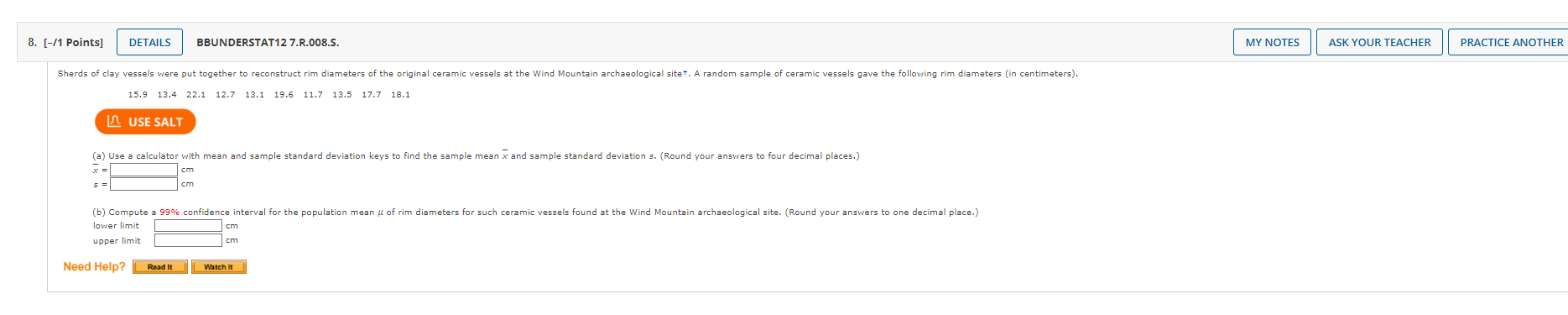
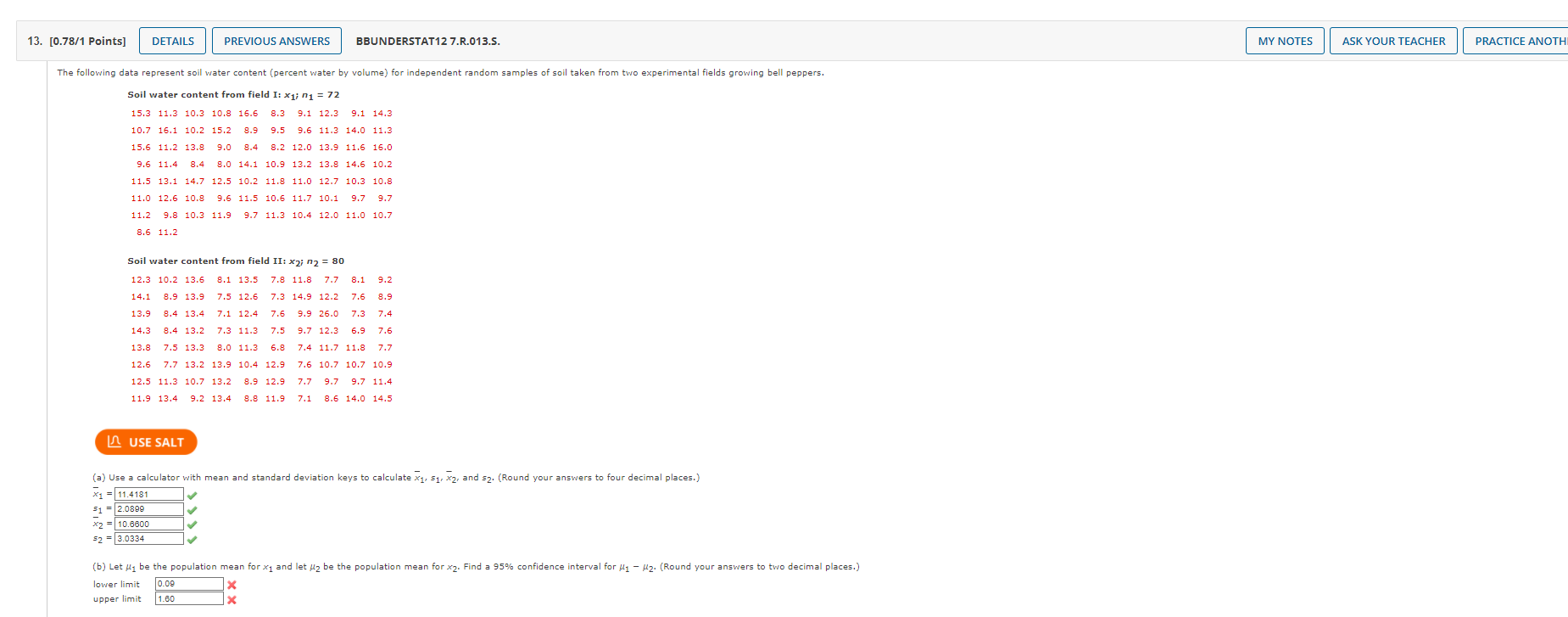
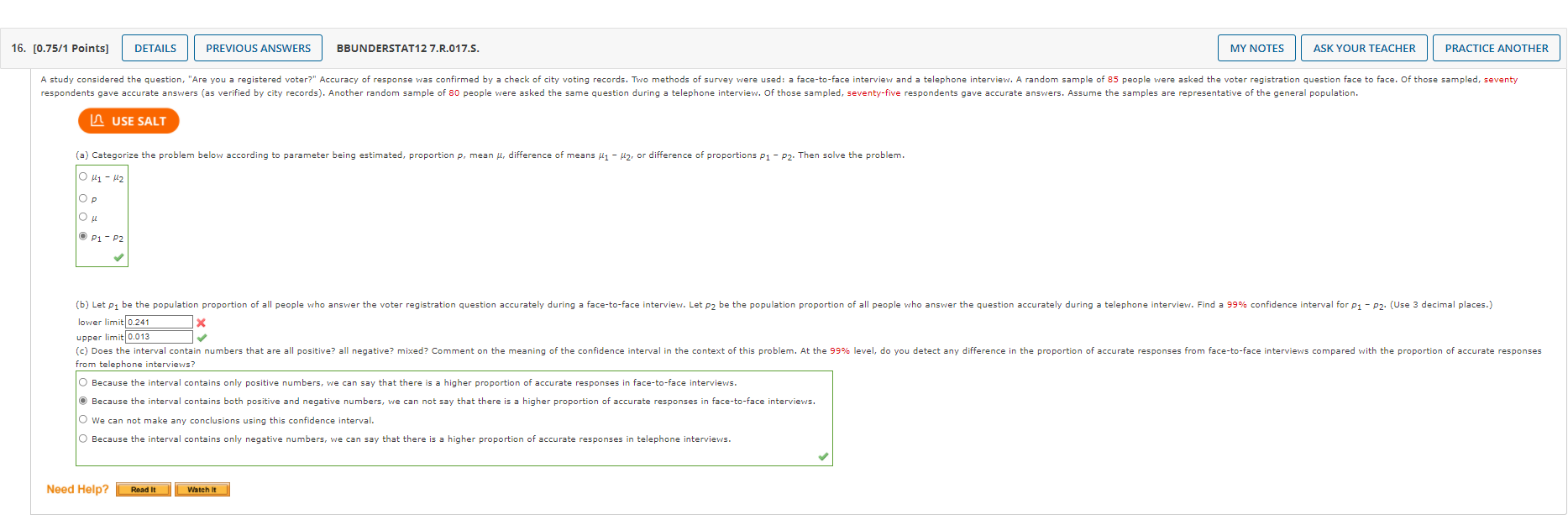
13. [0.5/1 Points] DETAILS PREVIOUS ANSWERS BBUNDERSTAT12 7.3.026.S. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER For this problem, carry at least four digits after the decimal in your calculations. Answers may vary slightly due to rounding. The National Council of Small Businesses is interested in the proportion of small businesses that declared Chapter 11 bankruptcy last year. Since there are so many small businesses, the National Council intends to estimate the proportion from a random sample. Let p be the proportion of small businesses that declared Chapter 11 bankruptcy last year. USE SALT (a) If no preliminary sample is taken to estimate p, how large a sample is necessary to be 99% sure that a point estimate p will be within a distance of 0.09 from p? (Round your answer up to the nearest whole number.) small businesses 205 (b) In a preliminary random sample of 30 small businesses, it was found that nine had declared Chapter 11 bankruptcy. How many more small businesses should be included in the sample to be 99% sure that a point estimate will be within a distance of 0.090 from p? (Round your answer up to the nearest whole number.) 172 Xmore small businesses Need Help? Read It 7. [0.87/1 Points] DETAILS PREVIOUS ANSWERS BBUNDERSTAT12 7.4.014.S. Independent random samples of professional football and basketball players gave the following information. Assume that the weight distributions are mound-shaped and symmetric. Weights (in lb) of pro football players: x; n = 21 247 261 255 251 244 276 240 265 257 252 282 256 250 264 270 275 245 275 253 265 272 Weights (in lb) of pro basketball players: x2; 2 = 19 202 200 220 210 192 215 221 216 228 207 225 208 195 191 207 196 182 193 201 I USE SALT (a) Use a calculator with mean and standard deviation keys to calculate x1, S1, x2, and S2. (Round your answers to four decimal places.) x = 259.7619 $1 X2 $2 12.0287 205.7368 = 12.7621 (b) Let be the population mean for x and let be the population mean for x2. Find a 99% confidence interval for - H2. (Round your answers to one decimal place.) lower limit upper limit 43.4 64.7 MY NOTES ASK YOUR TEACHER PRACTICE AN 8. [0.67/1 Points] DETAILS PREVIOUS ANSWERS BBUNDERSTAT12 7.4.016.MI.S. The following data represent petal lengths (in cm) for independent random samples of two species of iris. Petal length (in cm) of Iris virginica: x; n = 36 5.2 5.8 6.3 6.1 5.1 5.5 5.3 5.5 6.9 5.0 4.9 6.0 4.8 6.1 5.6 5.1 5.6 4.8 5.4 5.1 5.1 5.9 5.2 5.7 5.4 4.5 6.4 5.3 5.5 6.7 5.7 4.9 4.8 5.9 5.1 5.1 Petal length (in cm) of Iris setosa: x2; n = 38 1.6 1.6 1.4 1.5 1.5 1.6 1.4 1.5 1.4 1.2 1.3 1.5 1.3 1.6 1.9 1.6 1.4 1.3 1.7 1.5 1.5 USE SALT 1.2 1.4 1.7 1.0 1.7 1.9 1.6 1.4 1.6 1.5 1.6 1.2 1.9 1.5 (a) Use a calculator with mean and standard deviation keys to calculate x, sq, x2, and S2. (Round your answers to four decimal places.) 5.4805 51 0.5605 x2 1.4842 $2 0.2047 (b) Let be the population mean for x and let be the population mean for x2. Find a 99% confidence interval for - . (Round your answers to two decimal places.) lower limit 3.7 upper limit 4.2 MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER 13. [0.9/1 Points] DETAILS PREVIOUS ANSWERS BBUNDERSTAT12 7.4.026.MI.S. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER In the Focus Problem at the beginning of this chapter, a study was described comparing the hatch ratios of wood duck nesting boxes. Group I nesting boxes were well separated from each other and well hidden by available brush. There were a total of 465 eggs in group I boxes, of which a field count showed about 268 hatched. Group II nesting boxes were placed in highly visible locations and grouped closely together. There were a total of 783 eggs in group II boxes, of which a field count showed about 280 hatched. USE SALT (a) Find a point estimate p for p, the proportion of eggs that hatch in group I nest box placements. (Round your answer to four decimal places.) P1 0.5783 Find a 95% confidence interval for P. (Round your answers to three decimal places.) lower limit upper limit 0.531 0.621 (b) Find a point estimate 2 for P2, the proportion of eggs that hatch in group II nest box placements. (Round your answer to four decimal places.) P2 2. [-/1 Points] DETAILS BBUNDERSTAT12 7.R.002. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Suppose you are told that a 95% confidence interval for the average price of a gallon of regular gasoline in your state is from $2.93 to $4.21. Use the fact that the confidence interval for the mean is in the form x-E to x + E to compute the sample mean and the maximal margin of error E. (Round your answers to two decimal places.) x = $ E=$ Need Help? Read It Watch It 4. [-/1 Points] DETAILS BBUNDERSTAT12 7.R.004. Anystate Auto Insurance Company took a random sample of 376 insurance claims paid out during a 1-year period. The average claim paid was $1555. Assume = $256. Find a 0.90 confidence interval for the mean claim payment. (Round your answers to two decimal places.) lower limit upper limit Find a 0.99 confidence interval for the mean claim payment. (Round your answers to two decimal places.) lower limit $ upper limit $ Need Help? Read It MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER 5. [-/1 Points] DETAILS BBUNDERSTAT12 7.R.005. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Three experiments investigating the relation between need for cognitive closure and persuasion were performed. Part of the study involved administering a "need for closure scale" to a group of students enrolled in an introductory psychology course. The "need for closure scale" has scores ranging from 101 to 201. For the 66 students in the highest quartile of the distribution, the mean score was x = 177.30. Assume a population standard deviation of = 7.59. These students were all classified as high on their need for closure. Assume that the 66 students represent a random sample of all students who are classified as high on their need for closure. Find a 95% confidence interval for the population mean score on the "need for closure scale" for all students with a high need for closure. (Round your answers to two decimal places.) lower limit upper limit Need Help? Read It 6. [-/1 Points] DETAILS BBUNDERSTAT12 7.R.006.S. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER Three experiments investigating the relation between need for cognitive closure and persuasion were performed. Part of the study involved administering a "need for closure scale" to a group of students enrolled in an introductory psychology course. The "need for closure scale" has scores ranging from 101 to 201. For the 69 students in the highest quartile of the distribution, the mean score was x = 177.30. Assume a population standard deviation of = 8.31. These students were all classified as high on their need for closure. Assume that the 69 students represent a random sample of all students who are classified as high on their need for closure. How large a sample is needed if we wish to be 99% confident that the sample mean score is within 1.7 points of the population mean score for students who are high on the need for closure? (Round your answer up to the nearest whole number.) USE SALT students Need Help? Read It 7. [-/1 Points] DETAILS BBUNDERSTAT12 7.R.007.S. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER The Wind Mountain archaeological site is located in southwestern New Mexico. Wind Mountain was home to an ancient culture of prehistoric Native Americans called Anasazi. A random sample of excavations at Wind Mountain gave the following depths (in centimeters) from present-day surface grade to the location of significant archaeological artifacts+. 85 45 120 80 75 55 65 60 65 95 90 70 75 65 68 USE SALT (a) Use a calculator with mean and sample standard deviation keys to find the sample mean x and sample standard deviations. (Round your answers to four decimal places.) cm cm (b) Compute a 95% confidence interval for the mean depth at which archaeological artifacts from the Wind Mountain excavation site can be found. (Round your answers to one decimal place.) lower limit upper limit cm Need Help? Read It Watch It 8. [-/1 Points] DETAILS BBUNDERSTAT12 7.R.008.S. Sherds of clay vessels were put together to reconstruct rim diameters of the original ceramic vessels at the Wind Mountain archaeological sitet. A random sample of ceramic vessels gave the following rim diameters (in centimeters). 15.9 13.4 22.1 12.7 13.1 19.6 11.7 13.5 17.7 18.1 USE SALT (a) Use a calculator with mean and sample standard deviation keys to find the sample mean x and sample standard deviation s. (Round your answers to four decimal places.) cm (b) Compute a 99% confidence interval for the population mean of rim diameters for such ceramic vessels found at the Wind Mountain archaeological site. (Round your answers to one decimal place.) lower limit upper limit cm Need Help? Read It Watch It MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER 9. [-/1 Points] DETAILS BBUNDERSTAT12 7.R.009.S. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER A research group conducted an extensive survey of 3106 wage and salaried workers on issues ranging from relationships with their bosses to household chores. The data were gathered through hour-long telephone interviews with a nationally representative sample. In response to the question, "What does success mean to you?" 1538 responded, "Personal satisfaction from doing a good job." Let p be the population proportion of all wage and salaried workers who would respond the same way to the stated question. Find a 90% confidence interval for p. (Round your answers to three decimal places.) USE SALT lower limit upper limit Need Help? Read It Watch it 13. [0.78/1 Points] DETAILS PREVIOUS ANSWERS BBUNDERSTAT12 7.R.013.S. The following data represent soil water content (percent water by volume) for independent random samples of soil taken from two experimental fields growing bell peppers. Soil water content from field I: x1; n = 72 15.3 11.3 10.3 10.8 16.6 10.7 16.1 10.2 15.2 8.9 8.3 9.1 12.3 9.1 14.3 9.5 9.6 11.3 14.0 11.3 15.6 11.2 13.8 9.0 8.4 8.2 12.0 13.9 11.6 16.0 9.6 11.4 8.4 8.0 14.1 10.9 13.2 13.8 14.6 10.2 11.5 13.1 14.7 12.5 10.2 11.8 11.0 12.7 10.3 10.8 11.0 12.6 10.8 9.6 11.5 10.6 11.7 10.1 9.7 9.7 11.2 9.8 10.3 11.9 9.7 11.3 10.4 12.0 11.0 10.7 8.6 11.2 Soil water content from field II: x2; n2 = 80 12.3 10.2 13.6 8.1 13.5 7.8 11.8 7.7 8.1 9.2 14.1 8.9 13.9 7.5 12.6 13.9 8.4 13.4 7.1 12.4 7.6 9.9 26.0 14.3 8.4 13.2 7.3 11.3 7.5 13.8 7.5 13.3 8.0 11.3 12.6 7.7 13.2 13.9 10.4 12.9 12.5 11.3 10.7 13.2 8.9 12.9 11.9 13.4 9.2 13.4 8.8 11.9 6.8 7.3 14.9 12.2 7.6 8.9 7.3 7.4 9.7 12.3 6.9 7.6 7.4 11.7 11.8 7.7 7.6 10.7 10.7 10.9 7.7 9.7 9.7 11.4 7.1 8.6 14.0 14.5 USE SALT (a) Use a calculator with mean and standard deviation keys to calculate x1, S1, x2, and 52. (Round your answers to four decimal places.) x111.4181 $12.0899 x2 10.6600 $23.0334 (b) Let be the population mean for x1 and let be the population mean for x2. Find a 95% confidence interval for - 2. (Round your answers to two decimal places.) lower limit upper limit 0.09 1.60 MY NOTES ASK YOUR TEACHER PRACTICE ANOTH 16. [0.75/1 Points] DETAILS PREVIOUS ANSWERS BBUNDERSTAT12 7.R.017.S. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER A study considered the question, "Are you a registered voter?" Accuracy of response was confirmed by a check of city voting records. Two methods of survey were used: a face-to-face interview and a telephone interview. A random sample of 85 people were asked the voter registration question face to face. Of those sampled, seventy respondents gave accurate answers (as verified by city records). Another random sample of 80 people were asked the same question during a telephone interview. Of those sampled, seventy-five respondents gave accurate answers. Assume the samples are representative of the general population. USE SALT (a) Categorize the problem below according to parameter being estimated, proportion p, mean , difference of means - 2, or difference of proportions P1 - P2. Then solve the problem. P1-P2 (b) Let p be the population proportion of all people who answer the voter registration question accurately during a face-to-face interview. Let p2 be the population proportion of all people who answer the question accurately during a telephone interview. Find a 99% confidence interval for p1 - P2. (Use 3 decimal places.) lower limit 0.241 upper limit 0.013 (c) Does the interval contain numbers that are all positive? all negative? mixed? Comment on the meaning of the confidence interval in the context of this problem. At the 99% level, do you detect any difference in the proportion of accurate responses from face-to-face interviews compared with the proportion of accurate responses from telephone interviews? Because the interval contains only positive numbers, we can say that there is a higher proportion of accurate responses in face-to-face interviews. Because the interval contains both positive and negative numbers, we can not say that there is a higher proportion of accurate responses in face-to-face interviews. We can not make any conclusions using this confidence interval. Because the interval contains only negative numbers, we can say that there is a higher proportion of accurate responses in telephone interviews. Need Help? Read It Watch It