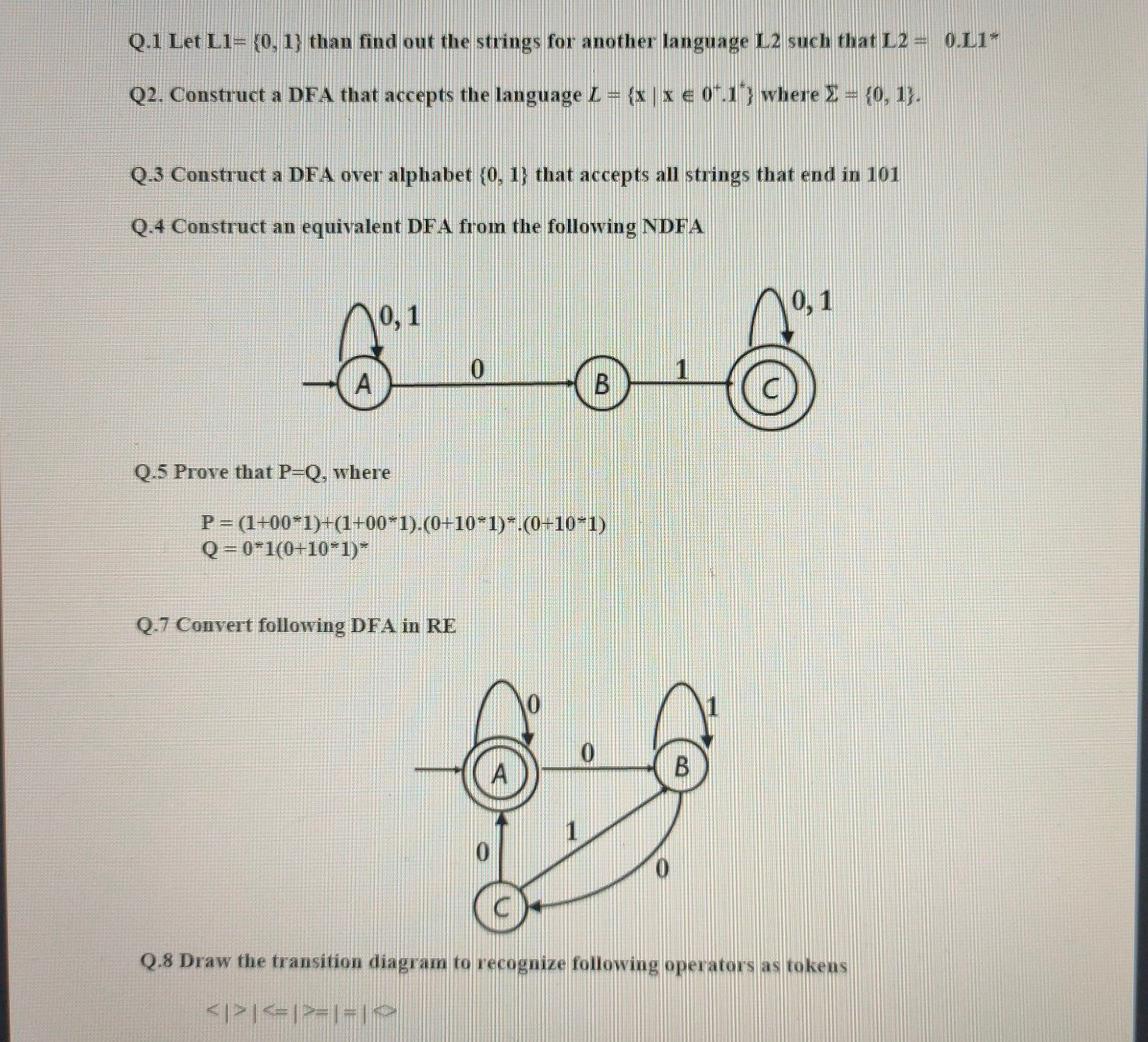
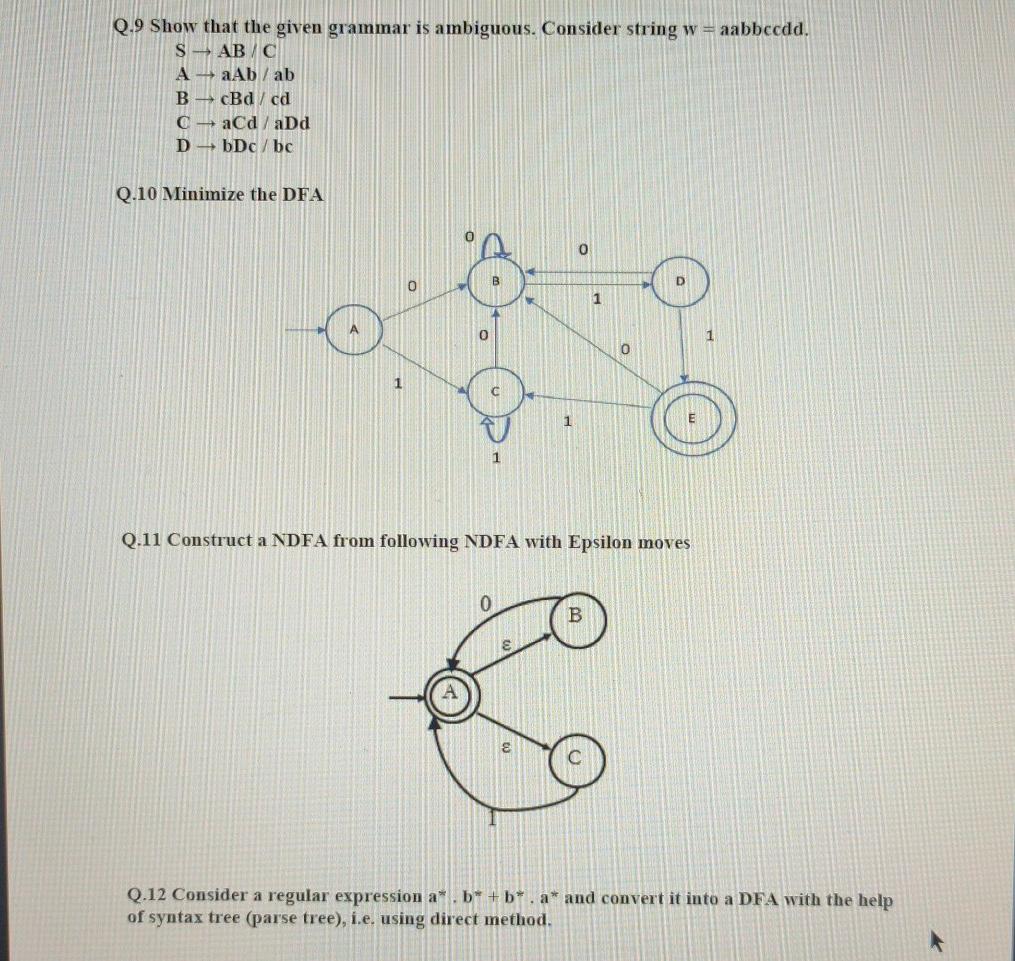
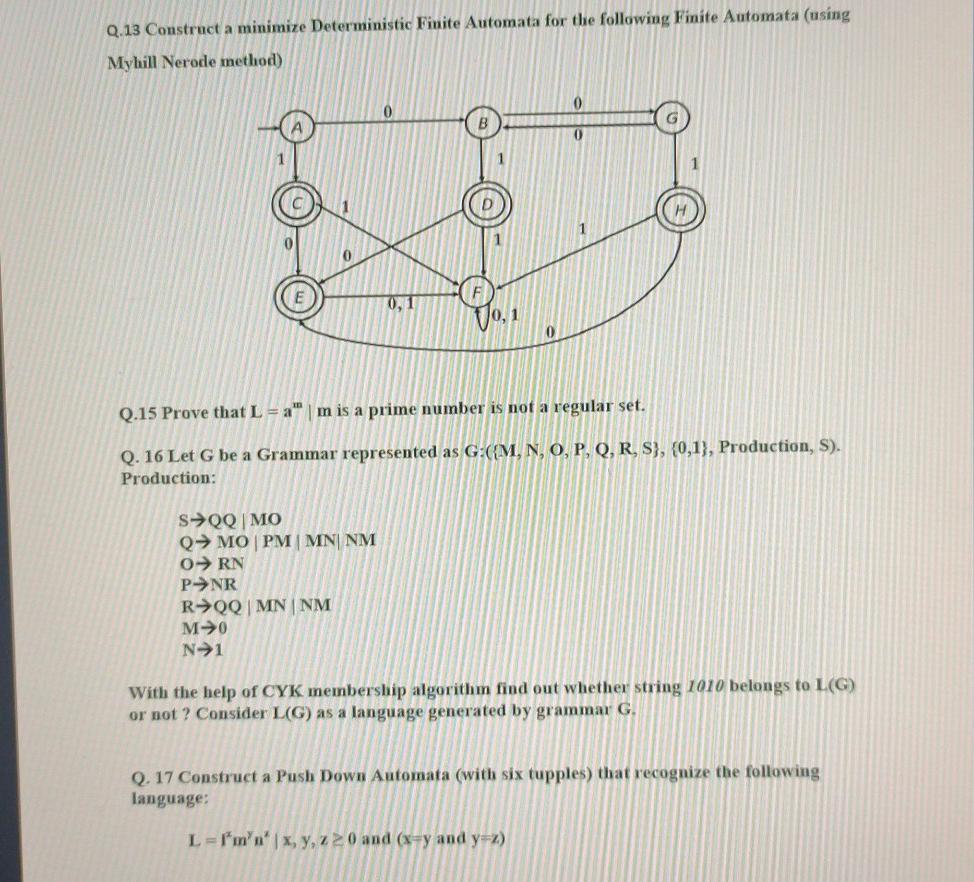
Q.1 Let Ll= {0, 1} than find out the strings for another language L2 such that L2 = 0.L1" Q2. Construct a DFA that accepts the language L = {x|x 04.1"} where I = {0, 1). Q.3 Construct a DFA over alphabet (0, 1) that accepts all strings that end in 101 Q.4 Construct an equivalent DFA from the following NDFA 0 Q.5 Prove that P=Q, where P = (1+00*1)+(1+00*1).(0+10*1)*.(0+10^1) Q = 0*100+10*1)* Q.7 Convert following DFA in RE B 0 Q.8 Draw the transition diagram to recognize following operators as tokeus =1=1 Q.9 Show that the given grammar is ambiguous. Consider string w=aabbccdd. S AB / C A aAb / ab B cBd / cd OaCd/aDd DbDc/bc Q.10 Minimize the DFA 0 0 D 1 0 O 1 1 1 Q.11 Construct a NDFA from following NDFA with Epsilon moves B Q.12 Consider a regular expression a". b* + b*. a* and convert it into a DFA with the help of syntax tree (parse tree), i.e. using direct method. Q.13 Construct a minimize Deterministic Finite Automata for the following Finite Automata (using Myhill Nerode method) 0 0 B 0 0 0 Q.15 Prove that L = am is a prime number is not a regular set. Q. 16 Let G be a Grammar represented as G:({M, N, O, P, Q, R, S}, {0,1), Production, S). Production: SQQIMO Q MOPM MN NM O RN PNR R>QQ | MN NM M>0 N>1 With the help of CYK membership algorithm find out whether string 1010 belongs to L(G) or not? Consider L(G) as a language generated by grammar G. Q. 17 Construct a Push Down Automata (with six tupples) that recognize the following language: L = f*m'n' | x, y, z 0 and (x=y and y=2)