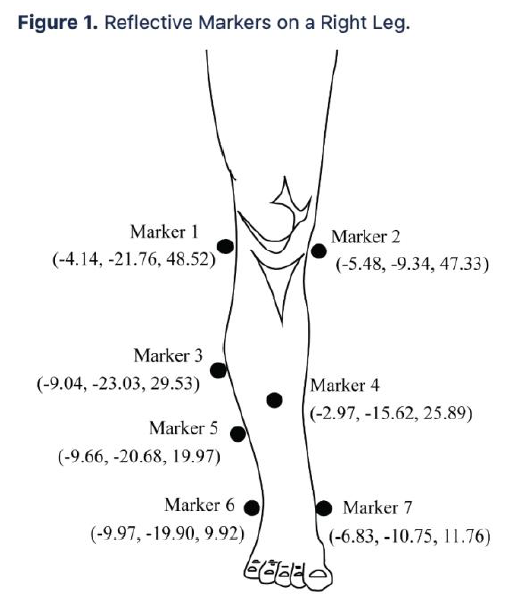
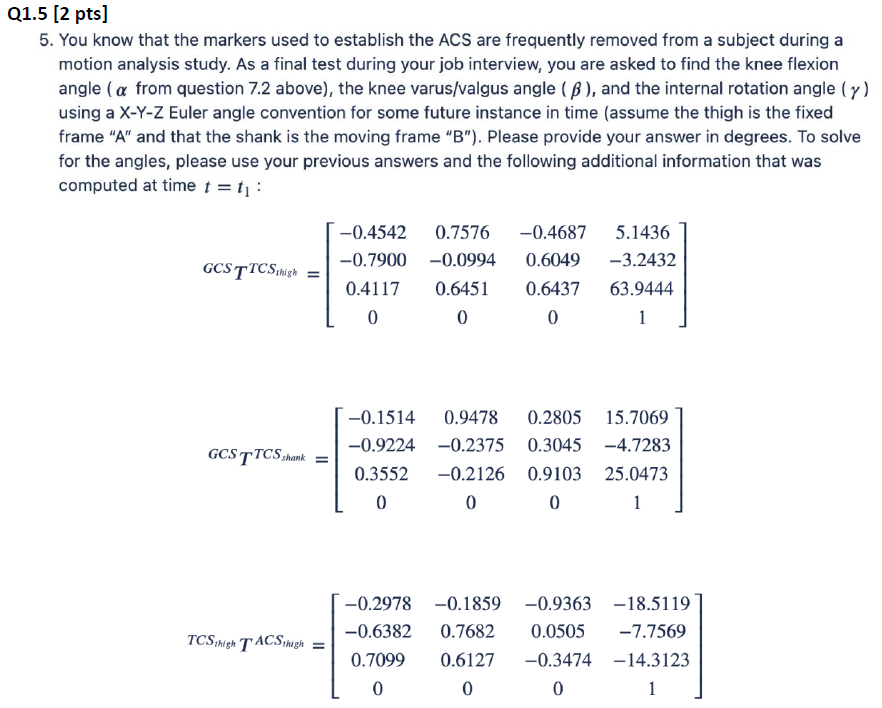
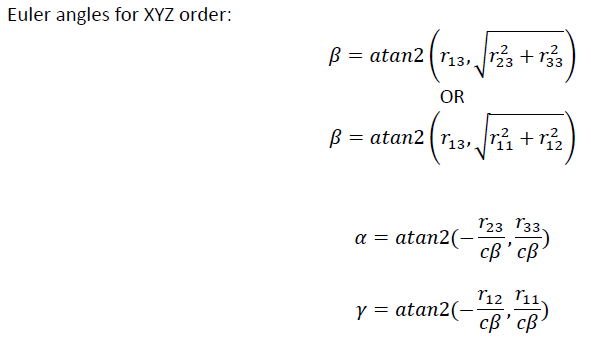
Q1.1 [0 pts] You are interviewing to work in a motion capture laboratory. During the job interview, you are presented with the 3-D marker convention shown in Figure 1. Since you have taken a biomechanics class, you feel confident in your ability to understand this marker convention. You quickly suspect that, for the shank, markers 3-5 are used to establish a Tracking Coordinate System (TCS) and that markers 1, 2, 6, and 7 are used to establish the Anatomic Coordinate System (ACS). You relay your suspicions to your interviewer, who is quite impressed with your ability. (NOTE: You have access to any computational tools during your interview). 1. You are told that markers 3-5 do form the TCS. Marker 4 is used as the origin. The x-axis is directed from marker 4 towards marker 3. The y-axis is directed anteriorly and is normal to the x-axis and the vector from marker 4 towards marker 5. The z-axis is normal to both the x-axis and the y-axis such that the axes form a right-handed basis. Using the values for the location the markers in the Global Coordinate System (GCS) shown in Figure 1, please derive the 4x4 homogeneous transformation matrix that expresses the TCS, with respect to the GCS ( GCS TTCS shank ) for the conditions shown in Figure 1. shank Figure 1. Reflective Markers on a Right Leg. Marker 1 (-4.14, -21.76, 48.52) Marker 2 (-5.48, -9.34, 47.33) Marker 3 (-9.04, -23.03, 29.53) Marker 4 (-2.97, -15.62, 25.89) Marker 5 (-9.66, -20.68, 19.97) Marker 6 (-9.97, -19.90, 9.92) Marker 7 (-6.83, -10.75, 11.76) Q1.2 [2 pts] 2. You are once again correct and are told that markers 1,2,6, and 7 do form the ACS (at this point, you're feeling good about the interview). You are told the following: "The origin for the shank ACS is the midpoint of markers 1 and 2. The z-axis is directed from the origin towards the midpoint of markers 6 and 7. The y-axis is directed anteriorly and is normal to the z-axis and a temp vector from marker 1 to marker 2. The x-axis normal to both the y-axis and z-axis and is directed medially." Using the values for the location the markers in the Global Coordinate System (GCS) shown in Figure 1, please derive the homogeneous transformation matrix that expresses the ACS shank with respect to the GCS ( GCST ACS shank) for the conditions shown in Figure 1. Q1.3 [2 pts] 3. Using your solutions to parts 1 and 2, please derive the transformation matrix that expresses the ACS shank with respect to TCS shank (TCS shank TACS shank ). Q1.4 [1 pts] 4. Which of the following transformation matrices are constant for the duration of an experiment (and therefore only need to be calculated once), and which vary with time? GCSTTCS shank GCSTTCS thigh GCST ACS shank GCST ACS thigh TCS shank TACS shank TCS thigh TACS thigh TCS thigh TTCS shank ACS thigh TACS shank Q1.5 [2 pts] 5. You know that the markers used to establish the ACS are frequently removed from a subject during a motion analysis study. As a final test during your job interview, you are asked to find the knee flexion angle (a from question 7.2 above), the knee varus/valgus angle (B), and the internal rotation angle (y) using a X-Y-Z Euler angle convention for some future instance in time (assume the thigh is the fixed frame "A" and that the shank is the moving frame "B"). Please provide your answer in degrees. To solve for the angles, please use your previous answers and the following additional information that was computed at time t = t: -0.4542 -0.7900 GCSTTCS thigh = 0.4117 0.7576 -0.0994 0.6451 -0.4687 5.1436 0.6049 -3.2432 0.6437 63.9444 0 0 0 1 GCS TTCS shank= 0 -0.1514 0.9478 0.2805 15.7069 -0.9224 -0.2375 0.3045 -4.7283 0.3552 -0.2126 0.9103 25.0473 0 0 1 TCS high TACS thigh = -0.2978 -0.1859 -0.9363 -18.5119 -0.6382 0.7682 0.0505 -7.7569 0.7099 0.6127 -0.3474 -14.3123 0 0 1 0 Euler angles for XYZ order: =atan2 13, 123 +133 (713. % +1%) OR 2 (113), 1/3) = atan2 13,+r 123 33. a = atan2(- y = atan2(- c'c 12 11. c' c