Q1.I need assistance solving the following continuous random variable questions.

Q2.Work on the arithmetic sequence questions.

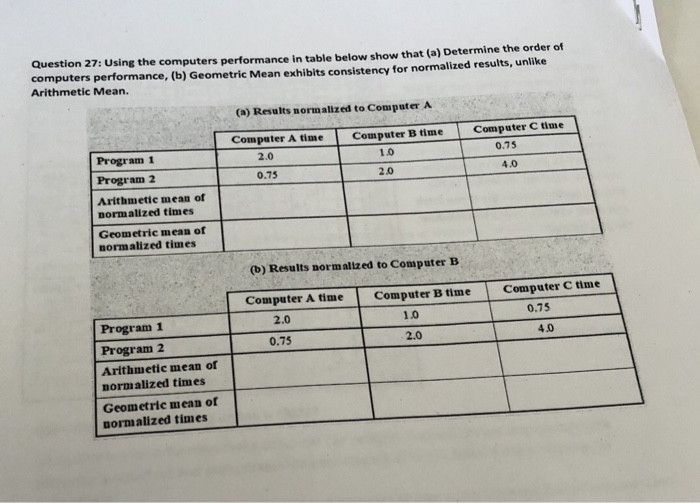
Regression 3, N-24 Regression Analysis: Concession1000 versus .. ndee100, Time, Trend2 Model Summary 5 R-sq R-sqladj) R-sq(pred) 16.7914 92.23% 91.07% 88.67%% Coefficients Term Coef SE Coef T-Value P-Value VIF Constant 180.0 15.1 11.92 0.000 Attendee100 -0.260 0.441 -0.59 0.562 1.03 Time 0.43 2.09 0.21 0.838 17.77 Trend2 0.2804 0.0809 3.47 0.002 17.68 Durbin-Watson Statistic Durbin-Watson Statistic = 1.83488 The manager's autocorrelation analysis included the following three regressions. Using Regression 3, do a test of positive first order autocorrelation. Choose whether the following are true or false. In general, the problem with autocorrelation is that time series data are correlated overtime, thus one knows a lot about Yt, by knowing the value of last periods Y...Yt-1. True 0 Fake search e e 9Calculate arithmetic and geometric means for stock A: Year A B C D E 1 9.7% 10.7% 70.3% 13.0% 23.1% 2 1.1% 23.4% -54.0% 15.2% -16.0% 3 -38.9% -32.1% 40.2% -40.0% 0.8% 4 34.5% 26.3% 94.5% 57.2% 13.7% 5 14.6% 11.8% 7.3% -4.2% 41.3% 6 3.7% 1.9% 25.5% 3.9% 5.7% Geometric mean equals 4.9%; arithmetic mean equals 3.4% Arithmetic mean equals 3.4%; geometric mean equals 5.6% Geometric mean equals 7.0%; arithmetic mean equals 7.5% Arithmetic mean equals 4.1%; geometric mean equals 1.3Determine whether the value is a discrete random variable, continuous random variable, or not a random variable. a. The number of light bulbs that burn out in the next week in a room with 16 bulbs b. The number of freethrow attempts before the rst shot is made c. The gender of college students d. The exad time it takes to evaluate 2?+ T2 e. The square footage of a house f. The amount of snowfall in December in City A a. Is the number of light bulbs that burn out in the next week in a room with 16 bulbs a discrete random variable, a continuous random variable, or not a random variable? 0 A. It is a discrete random variable. 0 B. It is a continuous random variable. 0 C. It is not a random variable. b. Is the number of freethrowI attempts before the rst shot is made a discrete random variable, a continuous random variable, or not a random variable? 0 A. It is a discrete random variable. 0 B. It is a continuous random variable. 0 C. It is not a random variable c. Is the gender of college students a discrete random variable, a continuous random variable, or not a random variable? 0 A. It is a continuous random variable. 0 B. It is a d'mcrete random variable. 0 C. It is not a random variable. d. Is the exact time it takes to evaluate 2? +?2 a discrete random variable. a continuous random variable. or not a random variable? 0 A. It is a continuous random variable. 0 B. It is a discrete random variable. 0 C. It is not a random variable. e. Is the square footage of a house a discrete random variable, a continuous random variable. or note random variable? 0 A. It is a continuous random variable 0 B. It is a discrete random variable. H r I| :. .mo .. "ml...\" .....:..L.I.. Question 27: Using the computers performance in table below show that (a) Determine the order of computers performance, (b) Geometric Mean exhibits consistency for normalized results, unlike Arithmetic Mean. (a) Results normalized to Computer A Computer A time Computer B time Computer C time Program 1 2.0 1.0 0.75 Program 2 0.75 2.0 4.0 Arithmetic mean of normalized times Geometric mean of normalized times (b) Results normalized to Computer B Computer A time Computer B time Computer C time Program 1 2.0 1.0 0.75 Program 2 0.75 2.0 4.0 Arithmetic mean of normalized times Geometric mean of normalized timesdy dx y(0) = 1 a) (5pts) Determine the solution of the above equation analytically b) (20 pts) Use Runge-Kutta second order Heun's method to solve the given equation over the interval [0, 12] with step size of h = 2 3 I X2 x2 S U a) y = b) Runge kutta Xi Yi ( True Value) Yi ( Runge Kutta) Error