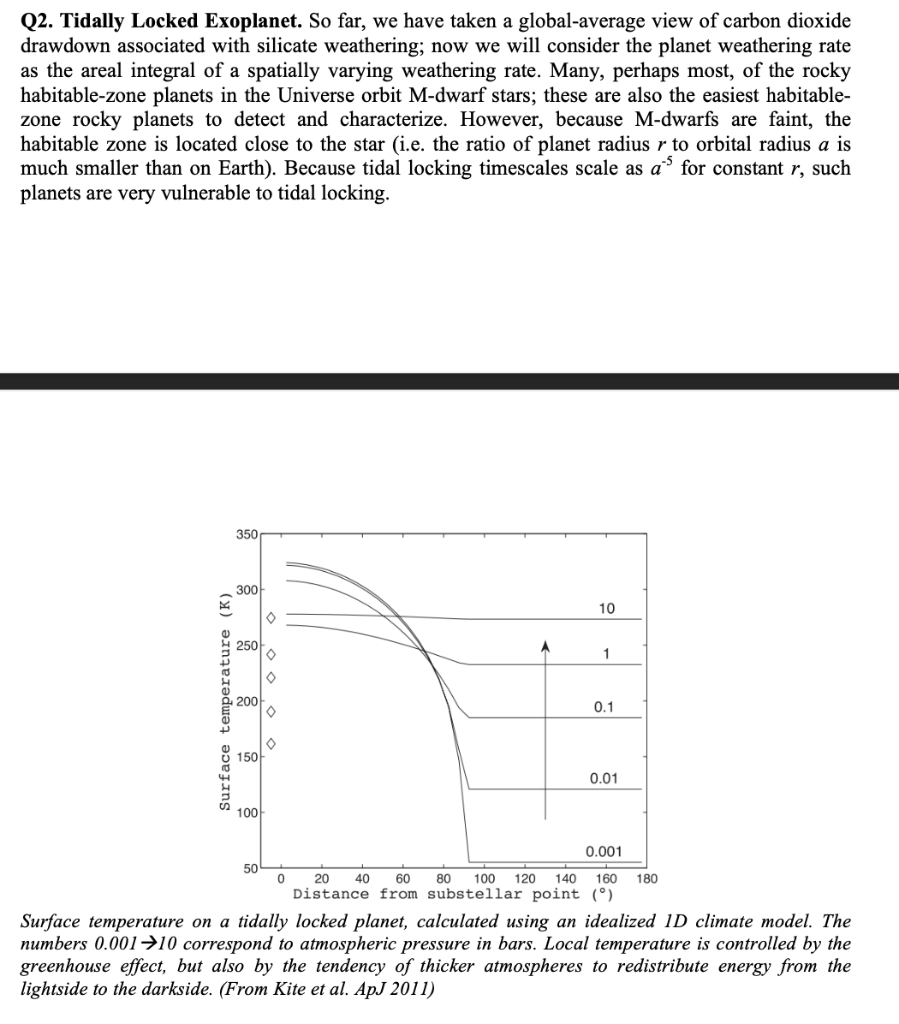

Q2. Tidally Locked Exoplanet. So far, we have taken a global-average view of carbon dioxide drawdown associated with silicate weathering; now we will consider the planet weathering rate as the areal integral of a spatially varying weathering rate. Many, perhaps most, of the rocky habitable-zone planets in the Universe orbit M-dwarf stars; these are also the easiest habitable- zone rocky planets to detect and characterize. However, because M-dwarfs are faint, the habitable zone is located close to the star (i.e. the ratio of planet radius r to orbital radius a is much smaller than on Earth). Because tidal locking timescales scale as a for constant r, such planets are very vulnerable to tidal locking. 350 300 10 250 A 1 Surface temperature (K) 200 0.1 150) 0.01 100 0.001 50 0 40 60 80 100 120 140 180 20 160 Distance from substellar point () Surface temperature on a tidally locked planet, calculated using an idealized ID climate model. The numbers 0.001~10 correspond to atmospheric pressure in bars. Local temperature is controlled by the greenhouse effect, but also by the tendency of thicker atmospheres to redistribute energy from the lightside to the darkside. (From Kite et al. ApJ 2011) (b ) Consider the tidally locked planet from the figure. (a) Assume weathering rate (kg/m/yr) scales as -E/RT w a e where E is activation energy and R is the gas constant and T is temperature in K. Assume an effective activation energy for weathering (effective including the effect of temperature on rainfall) of 74 kJ/mol, as for the previous homework. For the 0.01 bar tidally locked planet case, what is the ratio of weathering rate at the substellar point to weathering rate at 60 from the substellar point? Assuming mountain belts / tectonic uplift zones are randomly distributed with distance from the substellar point, comment on where on the planet most weathering occurs. Consider the likely effect of ice cover. (c) Now assume that the gas that is the principal constituent of the atmosphere is also the principal greenhouse gas. (This assumption was used to calculate the temperatures shown in the plot. This assumption is not true for the Earth, but is true for Mars, Venus, Triton, and arguably also Titan). Explain how the planet-integrated weathering rate changes as we increase pressure from 0.001 + 10 bars. (d) Is this hypothetical planet stable to a sudden two-fold step increase in the volcanic outgassing rate? Why? (e) Now assume that everything is the same as in (e), but the effective activation energy is now 1000 kJ/mol. Is this hypothetical planet stable to a sudden two-fold step increase in the volcanic outgassing rate? Why? Hint: Recall that the threshold surface temperature for moist greenhouse on a planet with water oceans is ~330K. Q2. Tidally Locked Exoplanet. So far, we have taken a global-average view of carbon dioxide drawdown associated with silicate weathering; now we will consider the planet weathering rate as the areal integral of a spatially varying weathering rate. Many, perhaps most, of the rocky habitable-zone planets in the Universe orbit M-dwarf stars; these are also the easiest habitable- zone rocky planets to detect and characterize. However, because M-dwarfs are faint, the habitable zone is located close to the star (i.e. the ratio of planet radius r to orbital radius a is much smaller than on Earth). Because tidal locking timescales scale as a for constant r, such planets are very vulnerable to tidal locking. 350 300 10 250 A 1 Surface temperature (K) 200 0.1 150) 0.01 100 0.001 50 0 40 60 80 100 120 140 180 20 160 Distance from substellar point () Surface temperature on a tidally locked planet, calculated using an idealized ID climate model. The numbers 0.001~10 correspond to atmospheric pressure in bars. Local temperature is controlled by the greenhouse effect, but also by the tendency of thicker atmospheres to redistribute energy from the lightside to the darkside. (From Kite et al. ApJ 2011) (b ) Consider the tidally locked planet from the figure. (a) Assume weathering rate (kg/m/yr) scales as -E/RT w a e where E is activation energy and R is the gas constant and T is temperature in K. Assume an effective activation energy for weathering (effective including the effect of temperature on rainfall) of 74 kJ/mol, as for the previous homework. For the 0.01 bar tidally locked planet case, what is the ratio of weathering rate at the substellar point to weathering rate at 60 from the substellar point? Assuming mountain belts / tectonic uplift zones are randomly distributed with distance from the substellar point, comment on where on the planet most weathering occurs. Consider the likely effect of ice cover. (c) Now assume that the gas that is the principal constituent of the atmosphere is also the principal greenhouse gas. (This assumption was used to calculate the temperatures shown in the plot. This assumption is not true for the Earth, but is true for Mars, Venus, Triton, and arguably also Titan). Explain how the planet-integrated weathering rate changes as we increase pressure from 0.001 + 10 bars. (d) Is this hypothetical planet stable to a sudden two-fold step increase in the volcanic outgassing rate? Why? (e) Now assume that everything is the same as in (e), but the effective activation energy is now 1000 kJ/mol. Is this hypothetical planet stable to a sudden two-fold step increase in the volcanic outgassing rate? Why? Hint: Recall that the threshold surface temperature for moist greenhouse on a planet with water oceans is ~330K








