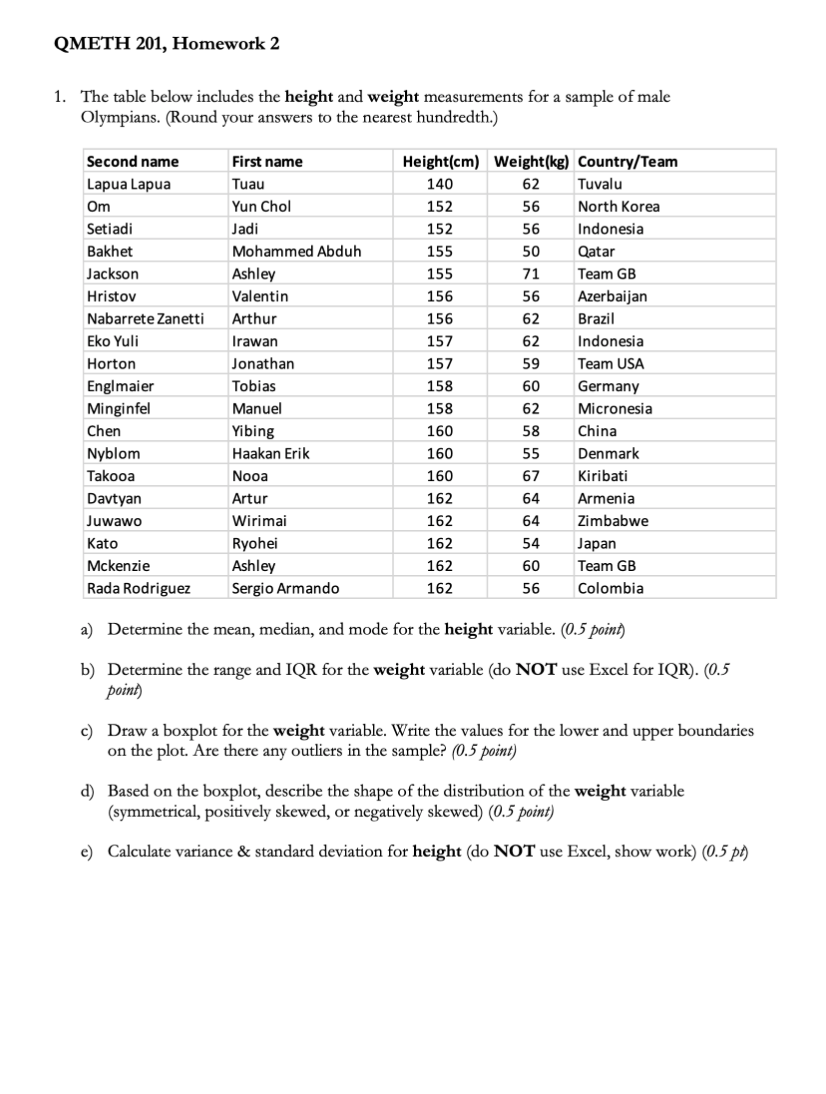
QMETH 201, Homework 2 1. The table below includes the height and weight measurements for a sample of male Olympians. (Round your answers to the nearest hundredth.) Second name First name Height(cm) Weight(kg) Country/Team Lapua Lapua Tuau 140 62 Tuvalu Om Yun Chol 152 56 North Korea Setiadi Jadi 152 56 Indonesia Bakhet Mohammed Abduh 155 50 Qatar Jackson Ashley 155 71 Team GB Hristov Valentin 156 56 Azerbaijan Nabarrete Zanetti Arthur 156 62 Brazil Eko Yuli Irawan 157 62 Indonesia Horton Jonathan 157 59 Team USA Englmaier Tobias 158 60 Germany Minginfel Manuel 158 62 Micronesia Chen Yibing 160 58 China Nyblom Haakan Erik 160 55 Denmark Takooa Nooa 160 67 Kiribati Davtyan Artur 162 64 Armenia Juwawo Wirimai 162 64 Zimbabwe Kato Ryohei 162 54 Japan Mckenzie Ashley 162 60 Team GB Rada Rodriguez Sergio Armando 162 56 Colombia a) Determine the mean, median, and mode for the height variable. (0.5 point) b) Determine the range and IQR for the weight variable (do NOT use Excel for IQR). (0.5 point c) Draw a boxplot for the weight variable. Write the values for the lower and upper boundaries on the plot. Are there any outliers in the sample? (0.5 point) d) Based on the boxplot, describe the shape of the distribution of the weight variable (symmetrical, positively skewed, or negatively skewed) (0.5 point) e) Calculate variance & standard deviation for height (do NOT use Excel, show work) (0.5 p/)QMETH 201, Homework 2 2. John is interested in how geographic region is related to politicians' political affiliation. John collected data (in 2019) about the political affiliations (parties) of US senators and the US regions they represent. Results are shown in the table below. The cell values are frequencies. (SHOW YOUR WORK and round to 3 decimal places) 2018 Region Democrats Republicans Independents Total Southeast 10 17 28 Southwest 1 5 6 OO West 7 11 18 Midwest 9 12 22 Northeast 15 6 22 Pacific 4 0 Total 46 51 3 100 a) Determine the probability a randomly selected senator is from the Southeast. (0.5 p/) b) Determine the probability a randomly selected Democratic senator is from the South (meaning either from SE or SW). (0.5 pf) c) Determine the probability a randomly selected Southern senator (meaning either from SE or SW) is Republican. (0.5 pf) d) Given your answers to Parts a), b), and c), are the two dimensions, Geography and Political Affiliation, statistically independent? (0.5 pf) e) Given your answer to Part d), is the distribution of Republican, Democratic, and Independent senators different or the same across various US Regions? (0.5 pf) 3. Now consider the same data (political affiliation of US Senators across geographical regions) for the year 2017. Only now the data is expressed in percentages in a two-way (joint distribution) table. 2017 Region Democrats Republicans Independents Total Southeast 0.09 0.18 0.01 0.28 Southwest 0.02 0.04 0 0.06 West 0.09 0.09 0 0.18 Midwest 0.1 0.11 0.01 0.22 Northeast 0.14 0.08 0 0.22 Pacific 0.03 0 0.01 0.04 Total 0.47 0.50 0.03 a) Determine the probability a randomly selected Republican senator is from the West (meaning either from W or MidW). (Round to 3 decimal places; 0.5 pts) b) Determine the probability a randomly selected senator from the South (meaning from SE and SW) is NOT affiliated with the Democratic party. (Round to 3 decimal places; 0.5 pts)QMEI'H 201, Homework 2 4. Within the We Huskies football organization, Sabrina works as a football analyst She believes that the outcome of the home january game against Oregon Ducks will be related toweather conditions that prevail in Seattle on that day. Local weather station estimates the probability of sunny and dry weather to equal 0.35 and the probability of rainy and muddy weather at 0.42. (The third probability is associated with freezing and snowy weather.) Based on her longitudinal analysis of team performance, Sabrina also estimates the following probabilities for the January game: 0.80 Huskies win if the weather is sunny and dry; 0.60 Ducks win if the weather is rainy and muddy; and equal chances of winning if the weather is freezing and snowy. If the Ducks win the game, determine the probability the weather was rainy and muddy. (HINT: start with a Venn diagram) (1.5m) 5. UW's Foster School of Business students have many talents, including ability to speak a foreign language. Below are the probabilities that correspond to students' ability to speak 1, 2 or 3 foreign matures (2W). Spanish = 0.33 Both Spanish and French = 0.06 All three languages = 0.02 French I 0.25 Both Spanish and Chinese I 0.11 Chinese = 0.24 Both French and Chinese = 0.07 a) Construct the associated Venn diagram with all probabilities specied. (HINT: start with the idea that Pr(S n F n C) = 0.02 and then work your way through the rest ofthe diagram). {fpu'm} Next, you select one UW Foster student at random for an interviews; detemaine the probabilityr s/he speaks b) Am: of the three languages [0.5Mk) c} Exactly one of the three languages (0.5phb) d) Exactly two of the three languages {0.5Mh')