
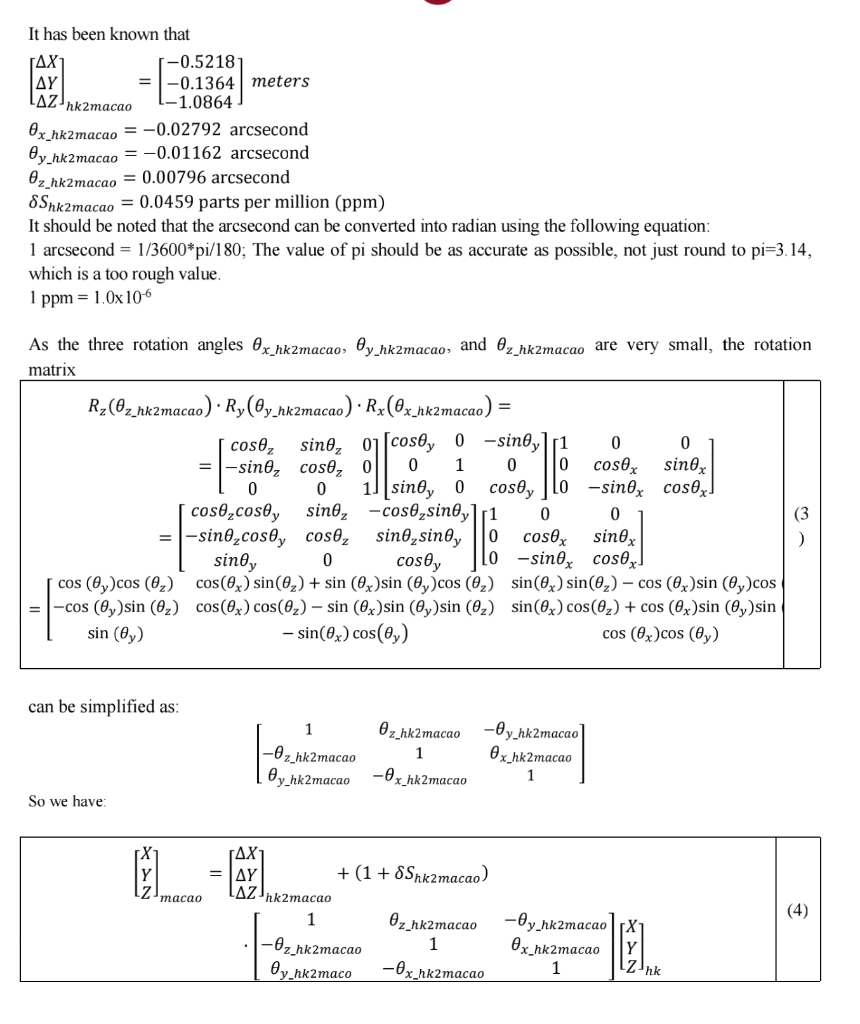


Question 1. 3D Coordinate conformal transformation is frequently used in geodesy and land surveying. The geodetic datum transformation from Hong Kong geodetic coordinates system (ITRF96) to Macao geodetic coordinates system (ITRF2005) have the following rigorous formula: TAX = | (1 + 8Shk2macao) Rz(@z_hk2macao) Ry(@y_hk2macao) , , LAZ hk2macao macao (1) Rx(@x_hk2ma 9x_hk2maco) y EL hk The geodetic datum transformation from Macao geodetic coordinates system (ITRF2005) to Hong Kong geodetic coordinates system (ITRF96) should have the following rigorous formula: -1 = AL = (1 + 8Sitzmacno)" (R3 (Oxstamacas) "IR, (Oy samacao)"[R_CO-stamacao) = {El x_hk2macao Y -Z Ink y_hk2macao z_hk2macao macao AY LAZ hk2macao -1 = (1 + 8Shxzmacao)-4 [R:(Ox-ntemacao) "[RyCQy nezmacao)*(RCO ik2macao)** | x_hk2macao y_hk2 -(1 + 8Shk2macao)-1 [Rx(Ox_hkemacao)]*'[Ry(Oy.nkamacao)] [Ry(@z_hk2macao)]** AY LAZ hk2macao LAZ hk2macao It has been known that -0.5218 AY = -0.1364 meters -1.0864 Ox_hkzmacao = -0.02792 arcsecond Oy_hk2macao = -0.01162 arcsecond Oz_hk2macao = 0.00796 arcsecond 8Snk2macao = 0.0459 parts per million (ppm) It should be noted that the arcsecond can be converted into radian using the following equation: 1 arcsecond = 1/3600*pi/180; The value of pi should be as accurate as possible, not just round to pi=3. 14, which is a too rough value. 1 ppm = 1.0x106 0 As the three rotation angles Ox_hkamacao, Oy_hkzmacao, and @z_hkamacao are very small, the rotation matrix Ry(Oz_hkamacao) Ry(@y_hk2macao) Rx(@x_hk2macao) cosez sine, 0][cos@y 0 -sino,r1 0 0 = 1-sine, cose, o 0 1 0 cosex sinex 0 0 1] [sinoy 0 coso, LO-sinox cosex] cose,cos y sino, -cos@sinoy1r1 0 0 1-sine,cosy cosez sine,sinoy 0 cosex sinex sinoy 0 cos@y [0-sinox cosex. cos (Cy)cos (0) cos((x) sin((,) + sin (0x)sin (@y)cos (0) sin(x) sin((_) - cos Ox)sin (@y)cos -cos (Oy)sin () cos(x) cos((2) - sin (0x)sin (Oy)sin (0) sin(x) cos((z) + cos (ex)sin (Oy)sin sin (@y) - sin(0x) cos(@y) cos (@x)cos (@y) = can be simplified as: 1 -Oz_hk2macao @y_hk2macao z_hk2macao 1 -Ox_hk2macao -Oy_hk2macao Ox_hk2macao 1 So we have IL macao = | + (1 + SSnk2macao) AZ"hk2macao 1 Oz_hk2macao -Oz hk2macao 1 Oy_hk2maco -Ox_hk2macao (4) -Oy_hk2macao Ox_hk2macao 1 hk (e) (15 marks) Numerically calculate JAY LAZ . Simplify the macao2hk 1 -(1 + 8Snk2macao)-- [R_(Oxhk2macao)]"'[R, (Oy_nk2macao))""[R_(@z_fk2macao)" AY ]| LAZ hk2macao in equation (2) so that it can be simplified as LAZ macao2hk Question 1. 3D Coordinate conformal transformation is frequently used in geodesy and land surveying. The geodetic datum transformation from Hong Kong geodetic coordinates system (ITRF96) to Macao geodetic coordinates system (ITRF2005) have the following rigorous formula: TAX = | (1 + 8Shk2macao) Rz(@z_hk2macao) Ry(@y_hk2macao) , , LAZ hk2macao macao (1) Rx(@x_hk2ma 9x_hk2maco) y EL hk The geodetic datum transformation from Macao geodetic coordinates system (ITRF2005) to Hong Kong geodetic coordinates system (ITRF96) should have the following rigorous formula: -1 = AL = (1 + 8Sitzmacno)" (R3 (Oxstamacas) "IR, (Oy samacao)"[R_CO-stamacao) = {El x_hk2macao Y -Z Ink y_hk2macao z_hk2macao macao AY LAZ hk2macao -1 = (1 + 8Shxzmacao)-4 [R:(Ox-ntemacao) "[RyCQy nezmacao)*(RCO ik2macao)** | x_hk2macao y_hk2 -(1 + 8Shk2macao)-1 [Rx(Ox_hkemacao)]*'[Ry(Oy.nkamacao)] [Ry(@z_hk2macao)]** AY LAZ hk2macao LAZ hk2macao It has been known that -0.5218 AY = -0.1364 meters -1.0864 Ox_hkzmacao = -0.02792 arcsecond Oy_hk2macao = -0.01162 arcsecond Oz_hk2macao = 0.00796 arcsecond 8Snk2macao = 0.0459 parts per million (ppm) It should be noted that the arcsecond can be converted into radian using the following equation: 1 arcsecond = 1/3600*pi/180; The value of pi should be as accurate as possible, not just round to pi=3. 14, which is a too rough value. 1 ppm = 1.0x106 0 As the three rotation angles Ox_hkamacao, Oy_hkzmacao, and @z_hkamacao are very small, the rotation matrix Ry(Oz_hkamacao) Ry(@y_hk2macao) Rx(@x_hk2macao) cosez sine, 0][cos@y 0 -sino,r1 0 0 = 1-sine, cose, o 0 1 0 cosex sinex 0 0 1] [sinoy 0 coso, LO-sinox cosex] cose,cos y sino, -cos@sinoy1r1 0 0 1-sine,cosy cosez sine,sinoy 0 cosex sinex sinoy 0 cos@y [0-sinox cosex. cos (Cy)cos (0) cos((x) sin((,) + sin (0x)sin (@y)cos (0) sin(x) sin((_) - cos Ox)sin (@y)cos -cos (Oy)sin () cos(x) cos((2) - sin (0x)sin (Oy)sin (0) sin(x) cos((z) + cos (ex)sin (Oy)sin sin (@y) - sin(0x) cos(@y) cos (@x)cos (@y) = can be simplified as: 1 -Oz_hk2macao @y_hk2macao z_hk2macao 1 -Ox_hk2macao -Oy_hk2macao Ox_hk2macao 1 So we have IL macao = | + (1 + SSnk2macao) AZ"hk2macao 1 Oz_hk2macao -Oz hk2macao 1 Oy_hk2maco -Ox_hk2macao (4) -Oy_hk2macao Ox_hk2macao 1 hk (e) (15 marks) Numerically calculate JAY LAZ . Simplify the macao2hk 1 -(1 + 8Snk2macao)-- [R_(Oxhk2macao)]"'[R, (Oy_nk2macao))""[R_(@z_fk2macao)" AY ]| LAZ hk2macao in equation (2) so that it can be simplified as LAZ macao2hk










