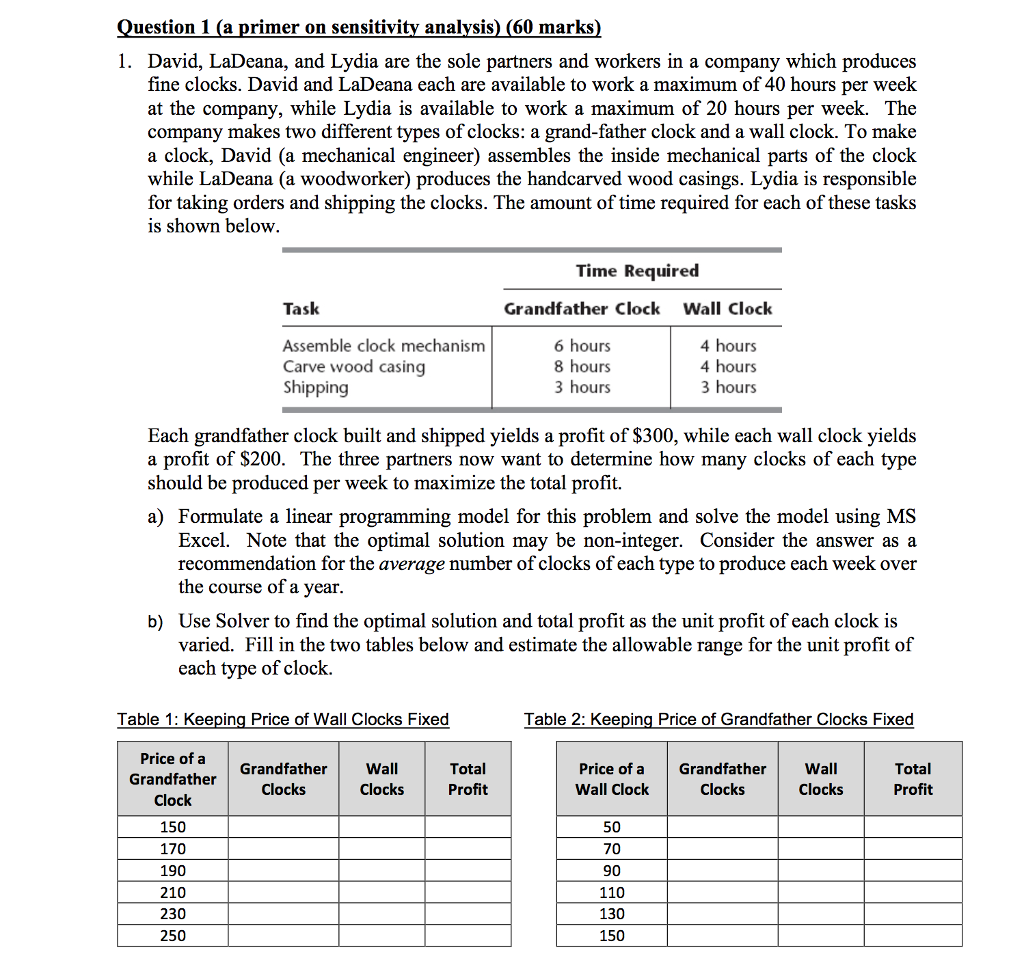
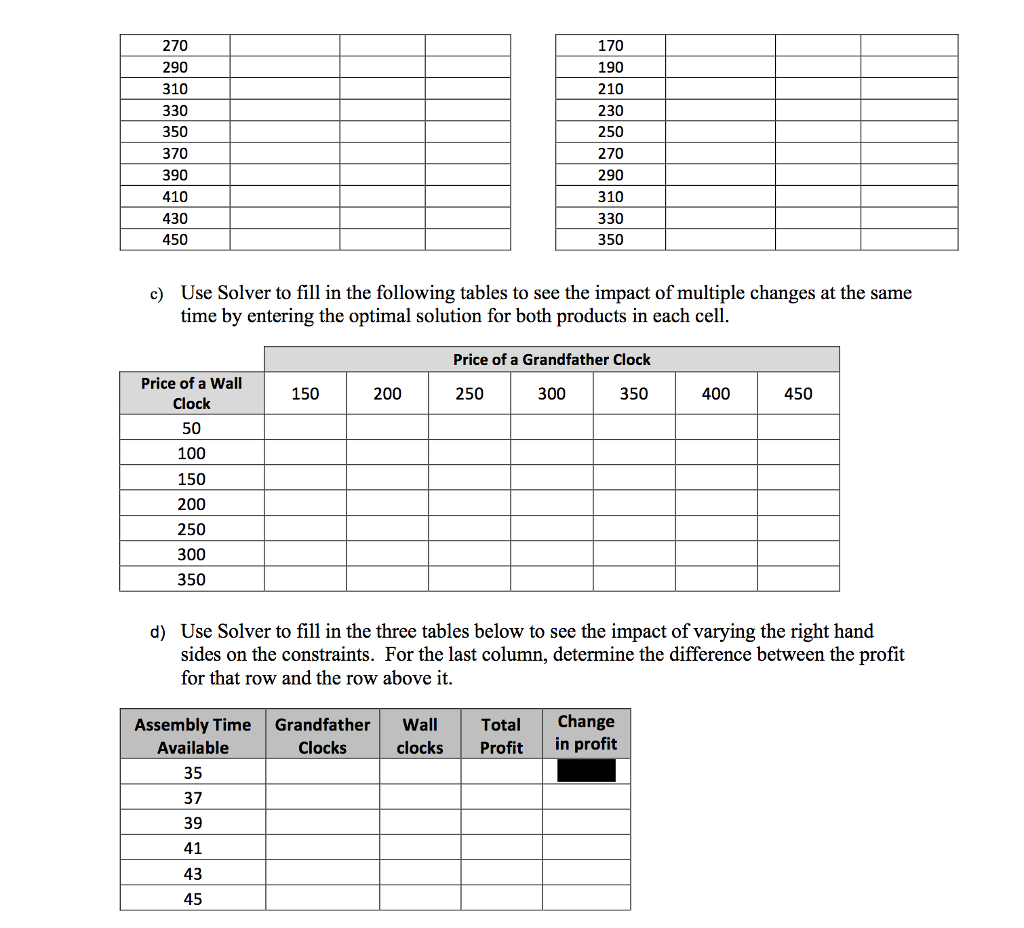
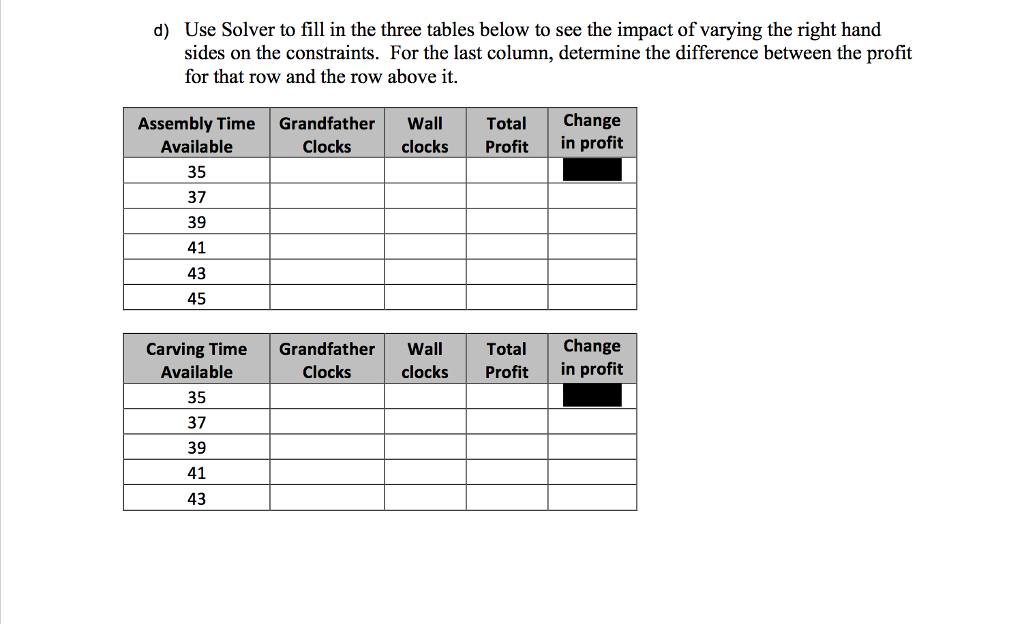
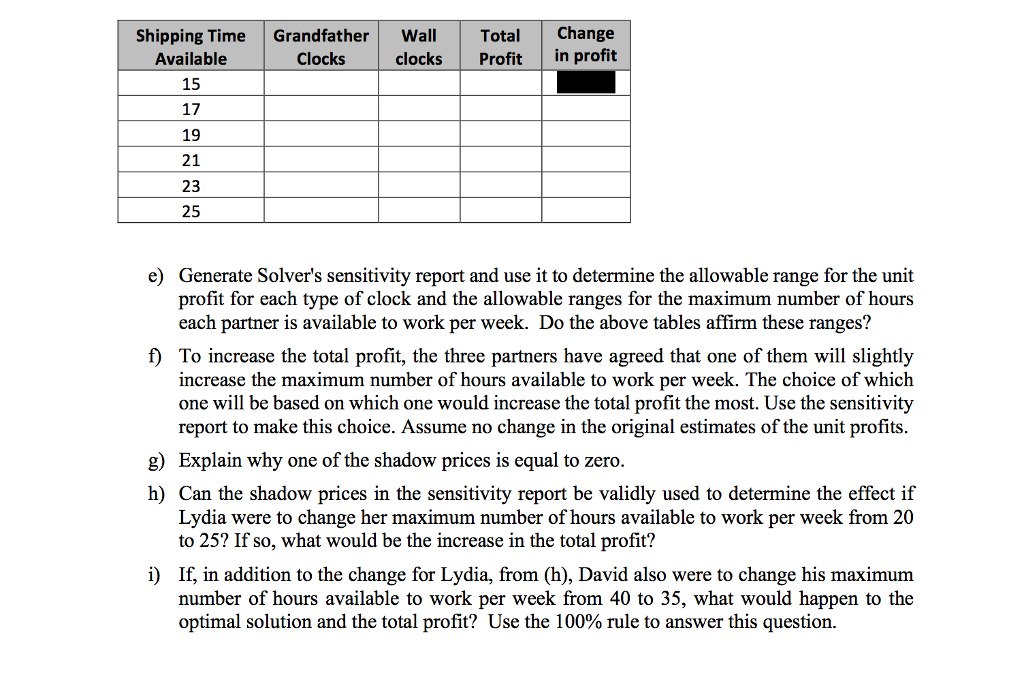
Question 1 (a primer on sensitivity analysis) (60 marks) 1. David, LaDeana, and Lydia are the sole partners and workers in a company which produces fine clocks. David and LaDeana each are available to work a maximum of 40 hours per week at the company, while Lydia is available to work a maximum of 20 hours per week. The company makes two different types of clocks: a grand-father clock and a wall clock. To make a clock, David (a mechanical engineer) assembles the inside mechanical parts of the clock while LaDeana (a woodworker) produces the handcarved wood casings. Lydia is responsible for taking orders and shipping the clocks. The amount of time required for each of these tasks is shown below. Time Required Task Grandfather Clock Wall Clock Assemble clock mechanism Carve wood casing Shipping 6 hours 4 hours 8 hours 4 hours 3 hours 3 hours Each grandfather clock built and shipped yields a profit of $300, while each wall clock yields a profit of $200. The three partners now want to determine how many clocks of each type should be produced per week to maximize the total profit. a) Formulate a linear programming model for this problem and solve the model using MS Excel. Note that the optimal solution may be non-integer. Consider the answer as a recommendation for the average number of clocks of each type to produce each week over the course of a year. b) Use Solver to find the optimal solution and total profit as the unit profit of each clock is varied. Fill in the two tables below and estimate the allowable range for the unit profit of each type of clock. Table 1: Keeping Price of Wall Clocks Fixed Table 2: Keeping Price of Grandfather Clocks Fixed Price of a Grandfather Grandfather Wall Clocks Clocks Total Profit Price of a Wall Clock Grandfather Clocks Wall Clocks Total Profit Clock 150 50 170 70 190 90 210 110 230 130 250 150 270 170 290 190 310 210 330 230 350 250 370 270 390 290 410 310 430 450 330 350 c) Use Solver to fill in the following tables to see the impact of multiple changes at the same time by entering the optimal solution for both products in each cell. Price of a Wall 150 200 300 Price of a Grandfather Clock 250 350 400 450 Clock 50 100 150 200 250 300 350 d) Use Solver to fill in the three tables below to see the impact of varying the right hand sides on the constraints. For the last column, determine the difference between the profit for that row and the row above it. Assembly Time Available Grandfather Clocks Wall Total clocks Profit Change in profit 35 37 39 41 43 45 d) Use Solver to fill in the three tables below to see the impact of varying the right hand sides on the constraints. For the last column, determine the difference between the profit for that row and the row above it. Assembly Time Grandfather Available Clocks Wall clocks Total Profit Change in profit 35 37 39 41 43 45 Carving Time Grandfather Wall Total Change Available Clocks clocks Profit in profit 35 37 39 41 43 Shipping Time Grandfather Wall Total Available Clocks clocks Profit Change in profit 15 17 19 21 23 25 e) Generate Solver's sensitivity report and use it to determine the allowable range for the unit profit for each type of clock and the allowable ranges for the maximum number of hours each partner is available to work per week. Do the above tables affirm these ranges? f) To increase the total profit, the three partners have agreed that one of them will slightly increase the maximum number of hours available to work per week. The choice of which one will be based on which one would increase the total profit the most. Use the sensitivity report to make this choice. Assume no change in the original estimates of the unit profits. g) Explain why one of the shadow prices is equal to zero. h) Can the shadow prices in the sensitivity report be validly used to determine the effect if Lydia were to change her maximum number of hours available to work per week from 20 to 25? If so, what would be the increase in the total profit? i) If, in addition to the change for Lydia, from (h), David also were to change his maximum number of hours available to work per week from 40 to 35, what would happen to the optimal solution and the total profit? Use the 100% rule to answer this question.