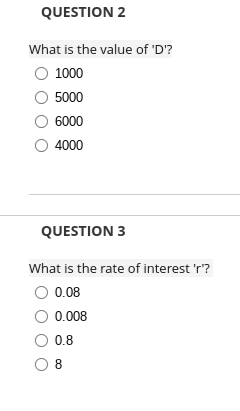
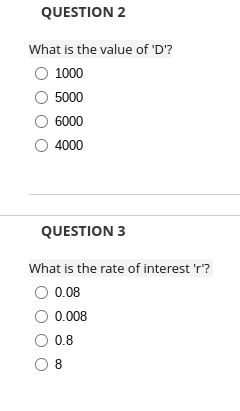
QUESTION 1 Consider the IVP dy - 3x = 2y satisfying y ( 0) = - What would be the appropriate dy -=g(x,y) using Euler's method dx 4 dx o approximate its solution, y =f (x) ? O 3x + 2y O - 3x + 2y Oxty O x-y QUESTION 2 For the above g (x, y ) you have found, what is g (x ,y ) ? O 01 O 2 OQUESTION 3 Note the difference between the approximate value given by Euler's method and the exact value above for x = 0.3. A better approximate value could have been obtained by taking which of the following / (there may be multiple answers)? Oh=0.2 Oh=0.5 O h=0.001 O h=0.02 QUESTION 4 Using Euler's method with /=0.1, approximate the solution of the above IVP at x = 0.1 (i.e., find y ). O 0.30 O 0.25 O 0.35 O 0.33QUESTION 5 Using Euler's method with / =0.1, approximate the solution of the above IVP at x = 0.2 (i.e., find y ,). O 0.39 O 0.49 O 0.25 O 0.37 QUESTION 6 Using Euler's method with / =0.1, approximate the solution of the above IVP at x = 0.3 (i.e., find y ). O 0.528 O 0.525 O 0.529 O 0.622QUESTION 7 dy As you may have noticed, -= 3x + 2y is a linear differential equation and can be brought to the standard linear form dx dy --2y=3x and can be solved exactly (so we did not have to use Euler's method or any other method to obtain dx approximate solution. We did this so that we can contrast the effectiveness of Euler's method by comparing it with the exact method.) dy The exact solution of the IVP - = 3x + 2y satisfying > (0) = - is: dx 4 2x (2x + 1) 4 2x (2x - 1) 4 2x 4 (2x + 1) 4 (2x + 1)QUESTION 8 Using the exact solution of the IVP above, compute y= f (x ) at x=0.3 O 0.622 O 0.528 O 0.525 O 0.629QUESTION 1 NOTE: All questions below refer to this problem. When Victor was born, his grandmother deposited $ 5000 in an account for him at 8 % annual interest compounded continuously. She plans to add to the account "continuously" at the rate of $ 100 a year. How much will there be for Victor when he is 18? State True or False: The differential equation used to solve this problem is: dA - =Ar+ D dt O True O FalseQUESTION 2 What is the value of 'D'? O 1000 O 5000 O 6000 O 4000 QUESTION 3 What is the rate of interest 'r'? O 0.08 O 0.008 O 0.8 O 8QUESTION 4 Find the initial condition, i.e., what is the value of A at time , = (? Le., what is A ( 0) ? O 5000 1000 O 6000 O 4000 QUESTION 5 The first-order differential equation dA =Ar+ D dt is both separable and linear. O True O FalseQUESTION 6 What is the most general solution of dA =rA + D dt for the above values of , and p? O A (t) = Co.081 - 12500 O A (t ) = Ce 0.08 + 12500 O A (D) = - Ce 0.081 + 12500 O A () = 125000e 0.081 - CQUESTION 7 Using the value of A (0) above, find the particular solution to the initial value problem. O A = 17500e .081 12500 O A = 17500e -0.08/ 12500 O A = 17500- 12500e 0.081 O A= 17500- 12500p -9.98t QUESTION 8 How much will there be for Victor when he is 18? O 61362 O 51362 O 71362 O 111362QUESTION 9 Find the integrating factor for dy 2x - - 6xy - xe*=0, x>0) dx O Op -#+ C O 1 + CQUESTION 10 Find the most general solution of the differential equation dy 3v = - 1x -e dx 2 O V= - + Ce 12 O V= + Ce 4 O + Ce& 8 O + Co- 4QUESTION 11 Treating it as a first-order linear differential equation, what is the integrating factor of dA =rA + D dt for the above values of $r$ and $D$? (NOTE: Make sure to bring the above differential equation to the standard linear form first.) O -0.081 O 0.081 O 0.81