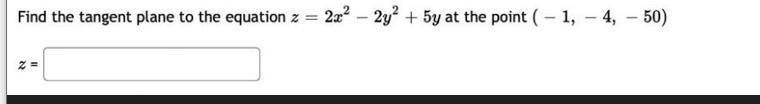
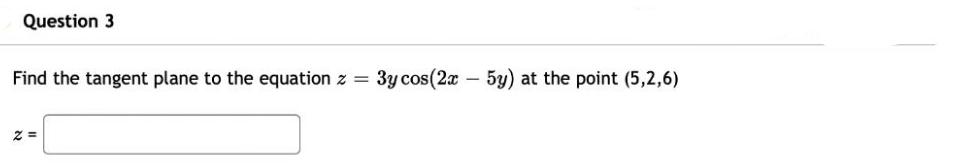
Find the tangent plane to the equation z = 2x Z= - - 2y + 5y at the point (-1,-4,50) Question 2 Find the tangent plane to the equation 2 = 2= 5e2 6y at the point (12, 24, 5) Question 3 Find the tangent plane to the equation z = Z= 3y cos(2x - 5y) at the point (5,2,6) Question 6 Find the direction in which the maximum rate of change occurs for the function f(x, y) = 2x sin(xy) at the point (1,2). Give your answer as a unit vector. Question 7 Find an equation for the tangent plane to the surface z + 3 = = xy cos(z) at the point (3, 1, 0)