Question
QUESTION 1 Given the model y = + 1 X 1 + 2 X 2 + 3 X 3 + and n = 20, what
QUESTION 1
- Given the model y = + 1X1 + 2X2 + 3X3 + and n = 20, what are the degrees of freedom on the error?
| A. | 16 | |
| B. | 19 | |
| C. | 17 | |
| D. | 20 |
QUESTION 2
Given y-hat = 25 + 7.5X1 +26.5X2 - 4.1X1X2, what is the predicted value of y
when X1 = 15 and X2 = 3?
| A. | 25 | |
| B. | 32.5 | |
| C. | 224.5 | |
| D. | 409.3 |
QUESTION 3
- Refer to problem 2. What is the residual when y = 29?
| A. | 31.5 | |
| B. | 3.5 | |
| C. | 32.5 | |
| D. | -3.5 |
QUESTION 4
- Given y = + 1X1 + 2X2 + 3X3 + , if the plot of the residuals against the predicted values of y yielded a plot with a fanning out shaped pattern then which assumption is violated?
| A. | normality | |
| B. | mean 0 | |
| C. | independence | |
| D. | constant variance |
QUESTION 5
- Given the model y = + 1X1 + 2X2 + 3X3 + if we plot y against X1 and get a parabola shaped curve then what does this suggest?
| A. | E() does not equal zero | |
| B. | an X12 term is needed | |
| C. | an X22 term is needed | |
| D. | constant variance violated |
QUESTION 6
Given the model y = + 1X1 + 2X2 + 3X12 + 4X22 + and with n = 20;
Which test do we use to test if the squared terms are significant to the model, when taken together?
| A. | Partial F-test | |
| B. | T-test | |
| C. | F-test | |
| D. | Durbin Watson |
QUESTION 7
Given the model y = + 1X1 + 2X2 + 3X12 + 4X22 + and with n = 20;
Which test do we use to test if the model is useful?
| A. | T-test | |
| B. | F-test | |
| C. | Partial F-test | |
| D. | Durbin Watson |
QUESTION 8
Given the model y = + 1X1 + 2X2 + 3X12 + 4X22 + and with n = 20
What is the null hypothesis for testing the squared terms as significant to the model when taken together?
| A. | Ho: 3 = 4 = 0 | |
| B. | Ha: at least one beta not equal to zero | |
| C. | Ho: 3 = 0 | |
| D. | Ho: 1 = 2 = 3 = 4 = 0 |
QUESTION 9
- Refer to question 8. We can reject Ho if the partial F test statistic is _________. (with n= 20)
| A. | >3.06 | |
| B. | ||
| C. | >3.68 | |
| D. |
QUESTION 10
- In the analysis of variance table (ANOVA) for any regression model, Sum of Squares error divided by degrees of freedom = ______________
| A. | mean square mode | |
| B. | R-squared | |
| C. | mean square error | |
| D. | F-value |
QUESTION 11
- In constructing a normal probability plot of the residuals, what shape is needed for normality to be satisfied?
| A. | linear | |
| B. | parabola shaped | |
| C. | bell shaped | |
| D. | S-shaped |
QUESTION 12
- In a multiple regression analysis, if the model provides a poor fit, then which of following will be true.
| A. | S2 will be small | |
| B. | SSE will be small | |
| C. | R2 will be close to 0 | |
| D. | all of these |
QUESTION 13
Which of the following variable selection techniques is a combination of the other 2 techniques that were discussed in the supplemental material folder?
| A. | Forward selection | |
| B. | Backward elimination | |
| C. | polynomial regression | |
| D. | Stepwise regression |
QUESTION 14
Given the model y = + 1X1 + 2X2 + 3X12 + 4X22 + and with n = 25, which test do we use to test if X2 is signficiant to the model?
| A. | F-test | |
| B. | Partial F-test | |
| C. | T-test | |
| D. | Polynomial test |
QUESTION 15
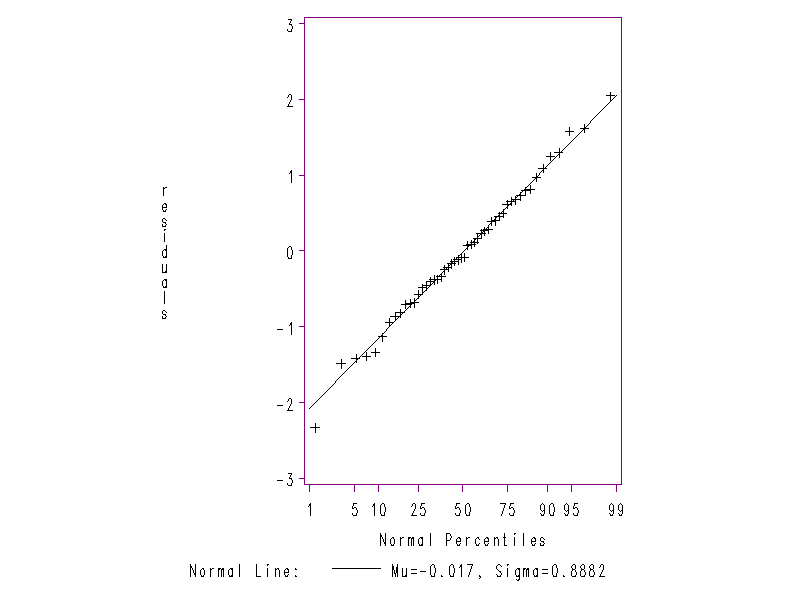
- Given the model y = + 1X1 + 2X2 + 3X3 + . We wish to check if the normality assumption is satisfed. Look at the normal probability plot that is in your handout, what can we conclude from this?
| A. | normality is satisfied | |
| B. | normality is seriously violated | |
| C. | constant variance is violated | |
| D. | constatn variance is satisfied |
QUESTION 16
- Given the model y = + 1X1 + 2X2 + 3X12 + 4X22 + and n = 25, what is the null hypothesis for testing if the model is useful?
| A. | Ho: 3 = 0 | |
| B. | Ho: at least one beta not equal to zero | |
| C. | Ho: 3 = 4= 0 | |
| D. | Ho: 1 = 2 = 3 = 4= 0 |
QUESTION 17
- In problem 16 we reject Ho if F test statistic is > ________
| A. | 2.87 | |
| B. | 3.10 | |
| C. | 2.84 | |
| D. | 2.76 |
QUESTION 18
- Given the model y = + 1X1 + 2X2 + with n = 125, SSE = 585, Fcal = 10 and p-value = 0.006; What is your conclusion when testing if the model is useful?
| A. | The result is inconclusive | |
| B. | The model is not useful | |
| C. | The model is useful | |
| D. | the variables are dependent |
QUESTION 19
Refer to problem 18. Now add 2 squared terms giving you a second order model.
y = + 1X1 + 2X2 + 3X12 + 4X22 + . Now with n =125, SSE = 334, What is your conclusion when testing if the squared terms are significant when taken together?
| A. | they are not significant | |
| B. | they are significant | |
| C. | the result is inclusive | |
| D. | none of these |
QUESTION 20
- Refer to Roman numeral I on your handout and answer question 20 below.
| A. | 10 and 27 | |
| B. | 3 and 34 | |
| C. | 6 and 31 | |
| D. | 4 and 34 |
QUESTION 21
- E() = 0
True
False
QUESTION 22
Var() = 2 and is non constant
True
False
QUESTION 23
- has a normal distribution
True
False
QUESTION 24
- The error terms are dependent.
True
False
QUESTION 25
- The range of R2 is -1 2
True
False
QUESTION 26
- The method of 'Least Squares is used to estimate the parameters in a regression model.
True
False
QUESTION 27
- The log transformation of the y variable will never achieve constant variance when that assumption is violated.
True
False
QUESTION 28
Refer to roman numeral II on your handout.
According to the model, what is the E(Y) when the car is a dodge?
| A. | o + 1X1 + 2IF + 3ID | |
| B. | o + 1X1 + 3 + | |
| C. | o + 1X1 | |
| D. | o + 1X1 + 3 |
QUESTION 29
- Refer to question 28. According to the model, what is D - C?
| A. | 3 | |
| B. | o + 1X1 + 3 | |
| C. | 2- 3 | |
| D. | 2 |
QUESTION 30
- Refer to question 28. According to the model, what is F - C
| A. | 3 | |
| B. | 2 | |
| C. | 2 - 3 | |
| D. | none of these |
QUESTION 31
- Refer to question 28. According to the model, what is F - D
| A. | 2 | |
| B. | 3 | |
| C. | 2 - 3 | |
| D. | none of these |
QUESTION 32
For the rest of the exam refer to the JMP problem in roman numeral 3 of your handout.
Write down the first order linear model.
| A. | y = E(Y) + | |
| B. | y = o + 1x1 + 2x2 + | |
| C. | y = o + 1x1 + 2x2 | |
| D. | none of these |
QUESTION 33
- Write down a second order linear model with interaction.
| A. | y = E(Y) + | |
| B. | y = + 1X1 + 2X2 + 3X12 + 4X22 + | |
| C. | y = + 1X1 + 2X2 + | |
| D. | y = + 1X1 + 2X2 + 3X12 + 4X22 + 5X1X2 + |
QUESTION 34
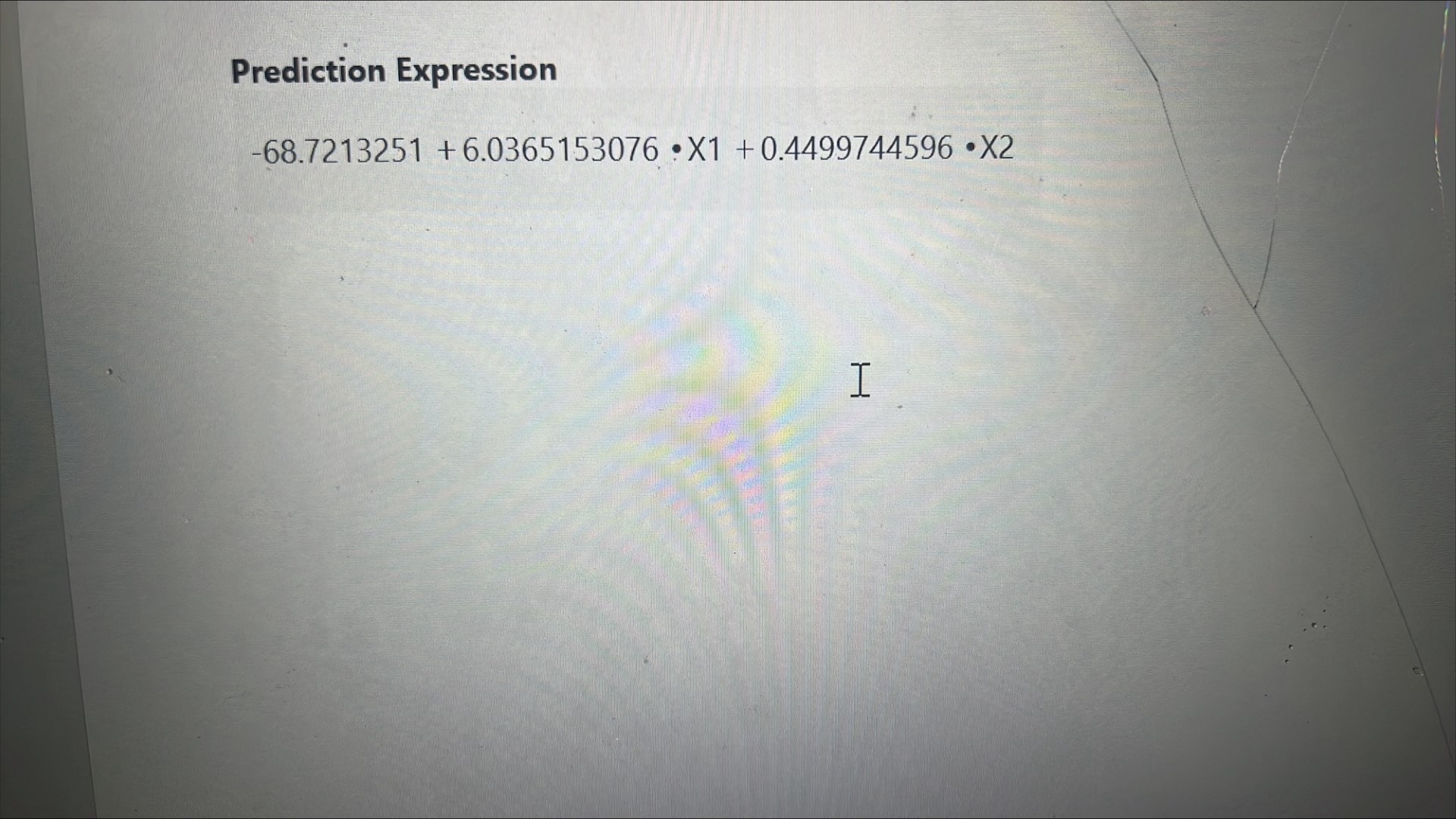
Now using the JMP output for the second order linear model with interaction do problems 34 through 56.
34. Write down the prediction equation. y^ =
| A. | -68.27133+6.03652X 1 +0.44997X 2 | |
| B. | -19.433779 - 3.73113X1 +0.67779X2 + 0.0576X12 - 0.0097X22 + 0.10643X1X2 | |
| C. | -19.433779 - 3.73113 + 0.67779 + 0.0576 - 0.0097 + 0.10643 | |
| D. | -91.2555 - 16.9756X 1 - 1.5128X 2- 0.4556X 1 2 - 0.0262X 2 2 + 0.4919X 1X 2 |
QUESTION 35
Refer to question 35 on your handout y^ =
QUESTION 36
- Refer to question 36 on your handout: y - y^ =
QUESTION 37
Refer to question 37 on your handout and only fill in the blanks of the interval.
What is the 95% CI for E(Y)? (__________, ____________)
example answer is 5, 10 and note no rounding.
QUESTION 38
Refer to question 38 on your handout and only fill in the blanks of the interval.
What is the 95% PI for Y? (__________, ____________)
example answer is 5, 10 and note no rounding.
QUESTION 39
- SSE = ____
QUESTION 40
- S2 = ____
QUESTION 41
- S = ________
QUESTION 42
Refer to question42 on your handout and only fill in the blanks of the interval.
What is the 95% CI for 2? (__________, ____________)
again no rounding and just numbers seperated by a comma
QUESTION 43
- In testing if the diameter of a tree is significant, state the null and alternative hypothesis
| A. | Ho: 1 = 0 vs. Ha: 1 not= 0 | |
| B. | Ho: 1 not= 0 vs. Ha: 1 = 0 | |
| C. | Ho: 2 = 0 vs. Ha: 2 not= 0 | |
| D. | none of these |
QUESTION 44
- Refer to question 44 on your handout. What is the test statistic?
QUESTION 45
Refer to question 45 on your handout. What is the correct decision?
QUESTION 46
- Refer to question 46 on your handout. Which of the following is the correct conclusion?
| A. | There is enough evidence to say that the diameter of a tree is significant to the model | |
| B. | There is not enough evidence to say that the diameter of a tree is significant to the model | |
| C. | There is enough evidence to say that the model is useful. | |
| D. | There is not enough evidence to say that the model is useful. |
QUESTION 47
- R2 = ____
QUESTION 48
- Which of the following best interprets R2?
| A. | about R2% of the y values are predicted by X. | |
| B. | The model is accurate about R2% of the time. | |
| C. | about R2% of the variation in the y values is explained by this model | |
| D. | X1 and X2 predict y about R2% of the time |
QUESTION 49
- In testing if the model is useful, state the null hypothesis.
| A. | Ho:3=0 | |
| B. | Ho:1 = 2 = 3= 4 = 5 =0 | |
| C. | Ho: 3= 4 = 5 =0 | |
| D. | none of these |
QUESTION 50
Refer to question 50 on your handout: What is the test statistic?
QUESTION 51
- Refer to question 51 on your handout, what is the correct decision?
| A. | Accept Ho | |
| B. | Do not reject Ho | |
| C. | Rejecth Ha | |
| D. | Reject Ho |
QUESTION 52
Refer to question 52 on your handout. Is the following statement ture or false?
There is enough evidecne to say the model is useful.
True
False
QUESTION 53
Refer to question 53 on your handout; State the null hypothesis.
| A. | Ho: 3= 4 =0 | |
| B. | Ho: at least one beta not equal to zero | |
| C. | Ho: 3= 4 = 5 =0 | |
| D. | none of these |
QUESTION 54
Refer to question 54 on the handout.
What is the correct decision?
| A. | Do not reject Ho | |
| B. | Reject Ho | |
| C. | Reject Ha |
QUESTION 55
Refer to question 55 on the handout; In conclusion there ________ enough evidence to say the squared terms and the interaction term are significant to the model when taken together?
| A. | is | |
| B. | is not | |
| C. | none of these |
QUESTION 56
For any given regression model and prediction equation if y = 99 and y-hat = 100 then E(Y) = ?
probability plot for number 15

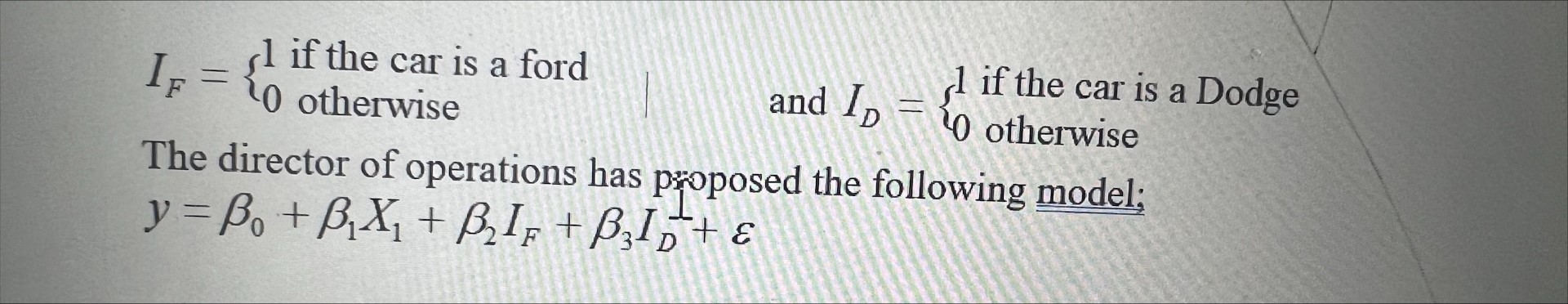
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


