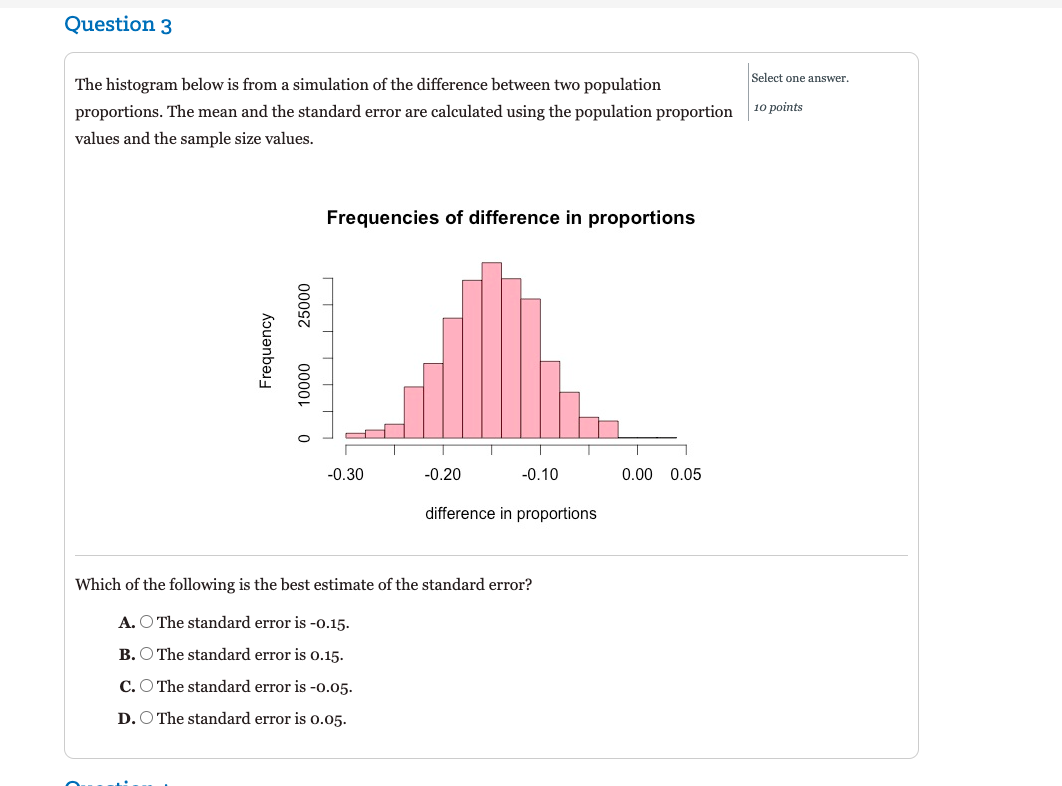
Question 1 In the article Coffee, Caffeine, and Risk of Depression Among Women in the September 2011 Select one answer. edition of the Archives of Internal Medicine, researchers investigated the relationship between |10 points caffeine consumption and depression among women. The participants in this study were older, with substantially lower rates of depression when compared to female teens. Researchers compared two groups of women (among others) in this study: those who do not drink coffee and those who routinely drink 4 or more cups of coffee each day. For the following question, a coffee drinker is a woman who drinks four or more cups each day. The depression rate for women who do not drink coffee is 6%. For the moment, we assume that this is the rate for coffee drinkers as well. We plan to survey 920 women who drink coffee and 1100 women who do not. We will determine the proportion of women who are depressed in each sample. Will the sampling distribution of differences between sample proportions be approximately normal? A. O Yes, a normal model is a good fit for this sampling distribution. B. O No, a normal model is not a good fit for this sampling distribution.Question 2 The histogram below is from a simulation of the difference between two population Select one answer. proportions. The mean and the standard error are calculated using the population proportion 10 points values and the sample size values. Frequencies of difference in proportions 25000 Frequency 10000 O -0.30 -0.20 -0.10 0.00 0.05 difference in proportions Which of the following is the best estimate of the population proportions? A. O The population proportions are 0.65 and 0.60. B. O The population proportions are 0.40 and 0.60. C. O The population proportions are 0.10 and 0.20. D. O The population proportions are 0.70 and 0.55.Question 3 The histogram below is from a simulation of the difference between two population Select one answer. proportions. The mean and the standard error are calculated using the population proportion 10 points values and the sample size values. Frequencies of difference in proportions 25000 Frequency 10000 O -0.30 -0.20 -0.10 0.00 0.05 difference in proportions Which of the following is the best estimate of the standard error? A. O The standard error is -0.15. B. O The standard error is 0.15. C. O The standard error is -0.05. D. O The standard error is 0.05.Skittles: The popular Skittles candy comes in 5 colors. According to the Skittles website, the Select one answer. colors are evenly distributed in the population of Skittle candies. So each color makes up 20% 10 points of the population. Suppose that we buy 2 small bags of Skittles. We determine the percentage of green Skittles in one bag and the percentage of orange Skittles in the other bag. Suppose that each bag contains 40 candies. We define the difference in sample proportions as "green" minus "orange." Which of the following will give a sample difference of 0.10? A. O 10 green and 6 orange B. O 4 green and 8 orange C. O 10 green and 10 orange Question 5 In a study at West Virginia University Hospital, researchers investigated smoking behavior of Type numbers in the boxes. cancer patients to create a program to help patients stop smoking. They published the results 10 points in Smoking Behaviors Among Cancer Survivors (January 2018, Journal of Oncology Practice). In this study, the researchers sent a 22-item survey to 1152 cancer patients. They collected demographic information (age, sex, ethnicity, zip code, level of education), clinical and smoking history, and information about quitting smoking. Of the 1152 patients who were mailed surveys, 230 patients responded. For various reasons, researchers used only 207 of the completed surveys. 32 out of 115 female cancer patients reported being past smokers, and 56 out of 92 male cancer patients reported being past smokers. Calculate the difference between the corresponding sample proportions P1 - P2 (female minus male). Round the answer to 4 decimal places