Question 1 Sample Proportion. In a Wakefield Research survey, respondents were asked if they ever hesitated to give a handshake because of a fear of
Question 1
Sample Proportion.In a Wakefield Research survey, respondents were asked if they ever hesitated to give a handshake because of a fear of germs. Of the respondents, 411 answered "yes" and 592 said "no". What is the sample proportion of yes responses rounded to three decimal places?
Group of answer choices
0.410
0.590
0.180
0.360
Question 2
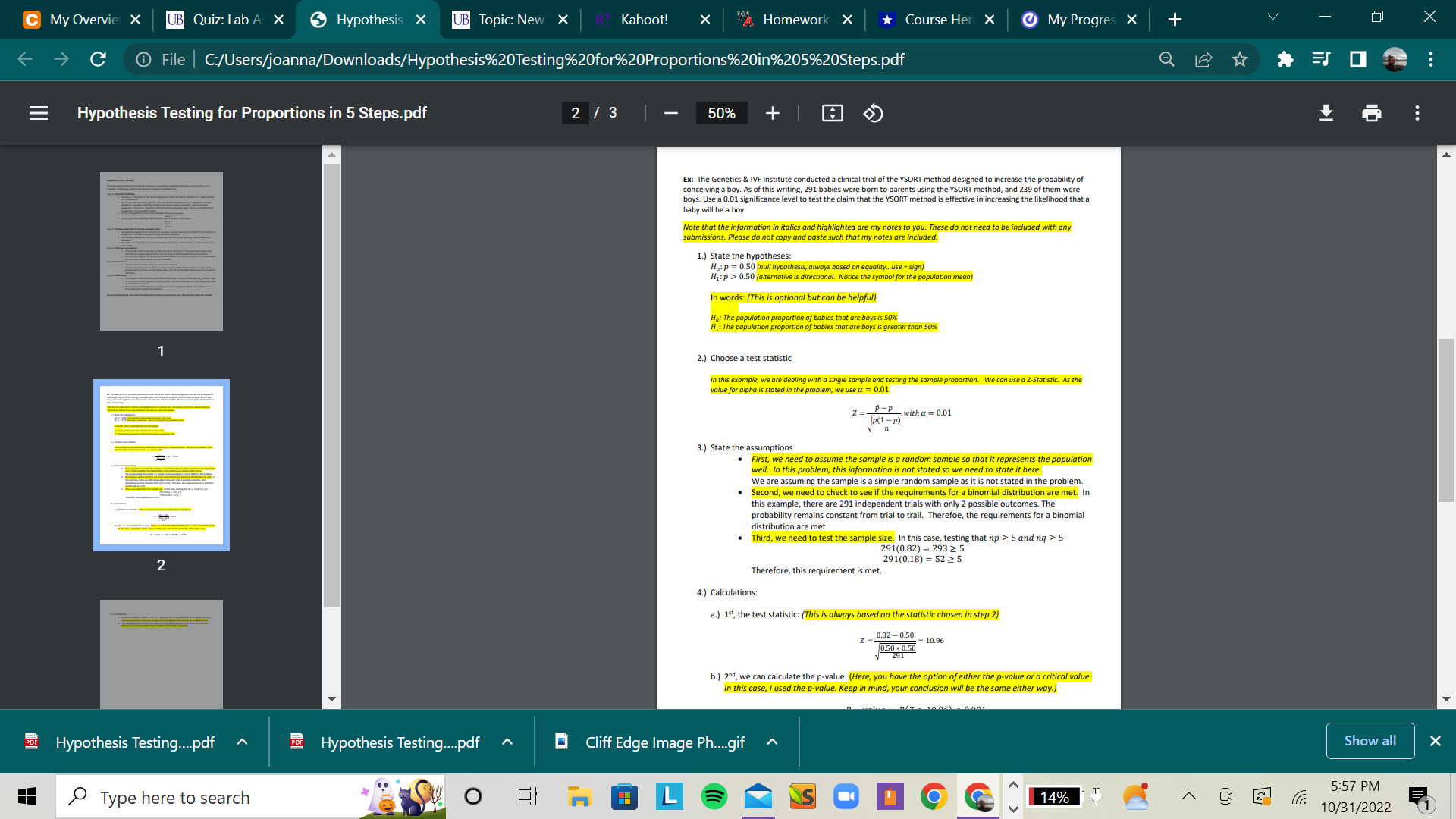
Hypothesis testing, Step 1: Stating the competing hypotheses. The Genetics & IVF Institute conducted a clinical trial of the YSORT method designed to increase the probability of conceiving a boy. As of this writing, 291 babies were born to parents using the YSORT method, and 239 of them were boys. Use a 0.01 significance level to test the claim that the YSORT method is effective in increasing the likelihood that a baby will be a boy.Fill in the blanksbelow to correctly state the competing hypotheses here:
H0: p = [ Select ] ["0.50", "0.82", "239", "291"]
H1:p [ Select ] ["greater than", "less than", "not equal to"] [ Select ] ["0.50", "0.82", "239", "291"]
Question 3
Hypothesis testing, Step 2: Deciding on a test statistic. The Genetics & IVF Institute conducted a clinical trial of the YSORT method designed to increase the probability of conceiving a boy. As of this writing, 291 babies were born to parents using the YSORT method, and 239 of them were boys. Use a 0.01 significance level to test the claim that the YSORT method is effective in increasing the likelihood that a baby will be a boy.Which of the following is the correct test statistic to test this claim?
Group of answer choices
Z-statistic for testing 1 proportion
Z-statistic for testing 2 proportions
Z-statistic for testing 1 mean
T-statistic for testing 1 mean
T-statistic for testing 2 means
Chi-square statistic for testing standard deviation
Question 4
Hypothesis testing, Step 3: Checking Assumptions. The Genetics & IVF Institute conducted a clinical trial of the YSORT method designed to increase the probability of conceiving a boy. As of this writing, 291 babies were born to parents using the YSORT method, and 239 of them were boys. Use a 0.01 significance level to test the claim that the YSORT method is effective in increasing the likelihood that a baby will be a boy.Given the test statistic from question #3, what assumptions are necessary to conduct this hypothesis test? Choose the correct values to fill in the following blanks
Requirement #1: The selected sample must be a [ Select ] ["simple random", "convenience", "cluster", ""] sample.
Requirement #2: The conditions for a [ Select ] ["binomial", "normal", "chi-square"] distribution must be met.
Requirement #3: Bothnp [ Select ] ["5", "25", "40"] andnq [ Select ] ["5", "25", "40"] so the the binomial distribution can be approximated with a normal distribution.
Question 5
Hypothesis testing, Step 3: Checking Assumptions(continued)The Genetics & IVF Institute conducted a clinical trial of the YSORT method designed to increase the probability of conceiving a boy. As of this writing, 291 babies were born to parents using the YSORT method, and 239 of them were boys. Use a 0.01 significance level to test the claim that the YSORT method is effective in increasing the likelihood that a baby will be a boy.Given the listed requirements fromtheprevious questions, are they all met.
Requirement #1: The selected sample must be a simple random sample: This is not mentioned in the question so in order to conduct this test, we need to assume this sample is a simple random sample. We will state it as such.
Requirement #2: The conditions for abinomialdistribution must be met.These requirements are met. There are 291 independent trials with the same probability from trial to trial and only two possible outcomes: boy or girl.
Requirement #3: Bothnp5andnq5so the the binomial distribution can be approximated with a normal distribution. This is very important and must be calculated each time to ensure that our binomial distribution is not overly skewed. If p, the proportion of successes is either very large or very small, the binomial distribution will be too skewed to approximate with a normal distribution. As such, we would need a different method to run this test. It is important to check BOTH parts of this.
1.) Calculate np. Enter the value for np below.
Question 6
Hypothesis testing, Step 3: Checking Assumptions(continued)The Genetics & IVF Institute conducted a clinical trial of the YSORT method designed to increase the probability of conceiving a boy. As of this writing, 291 babies were born to parents using the YSORT method, and 239 of them were boys. Use a 0.01 significance level to test the claim that the YSORT method is effective in increasing the likelihood that a baby will be a boy.Given the listed requirements fromtheprevious questions, are they all met.
Requirement #3: Bothnp5andnq5so the the binomial distribution can be approximated with a normal distribution. This is very important and must be calculated each time to ensure that our binomial distribution is not overly skewed. If p, the proportion of successes is either very large or very small, the binomial distribution will be too skewed to approximate with a normal distribution. As such, we would need a different method to run this test. It is important to check BOTH parts of this.
2.) Calculate nq. Enter the value for nq below.
Question 7
Hypothesis testing, Step 3: Checking Assumptions(conclusion)The Genetics & IVF Institute conducted a clinical trial of the YSORT method designed to increase the probability of conceiving a boy. As of this writing, 291 babies were born to parents using the YSORT method, and 239 of them were boys. Use a 0.01 significance level to test the claim that the YSORT method is effective in increasing the likelihood that a baby will be a boy.Given the listed requirements fromtheprevious questions, are they all met.
Requirement #1: The selected sample must be a simple random sample: This is not mentioned in the question so in order to conduct this test, we need to assume this sample is a simple random sample. We will state it as such.
Requirement #2: The conditions for abinomialdistribution must be met.These requirements are met. There are 291 independent trials with the same probability from trial to trial and only two possible outcomes: boy or girl.
Requirement #3: Bothnp5andnq5so the the binomial distribution can be approximated with a normal distribution. This is very important and must be calculated each time to ensure that our binomial distribution is not overly skewed. If p, the proportion of successes is either very large or very small, the binomial distribution will be too skewed to approximate with a normal distribution. As such, we would need a different method to run this test. It is important to check BOTH parts of this.
True/False: If we assume the selected sample is a simplerandom sample, then all of the requirements in this case are met to conduct the hypothesis test.
Group of answer choices
True
False
Question 8
Hypothesis testing, Step 4: Calculating the test statistic. The Genetics & IVF Institute conducted a clinical trial of the YSORT method designed to increase the probability of conceiving a boy. As of this writing, 291 babies were born to parents using the YSORT method, and 239 of them were boys. Use a 0.01 significance level to test the claim that the YSORT method is effective in increasing the likelihood that a baby will be a boy.What is the value of theteststatistic needed to test this claim?
1: Find the value of the test statistic following the instructions below:
a) Press STAT & scroll to TESTS & select "1-PropZTest..." (option 5 in TI83Plus) & pressEnter (for a hypothesis test of a claim involving one population).
b) Enter the following:
- po = claimed value of the population proportion. It's the same value used in nullhypothesis.
- x = number of successes calculated as n p = where n = sample size, p = sampleproportion. The sample proportion is obtained by: p = 239/291
- n = sample size, which is 291
c) Highlight ">P0 and press ENTER
d) Highlight "Calculate" and press ENTER & make note of the calculations as you will needthem below.
Enter the value of the Z-Test statistic here. Round to two decimal places if necessary.
Question 9
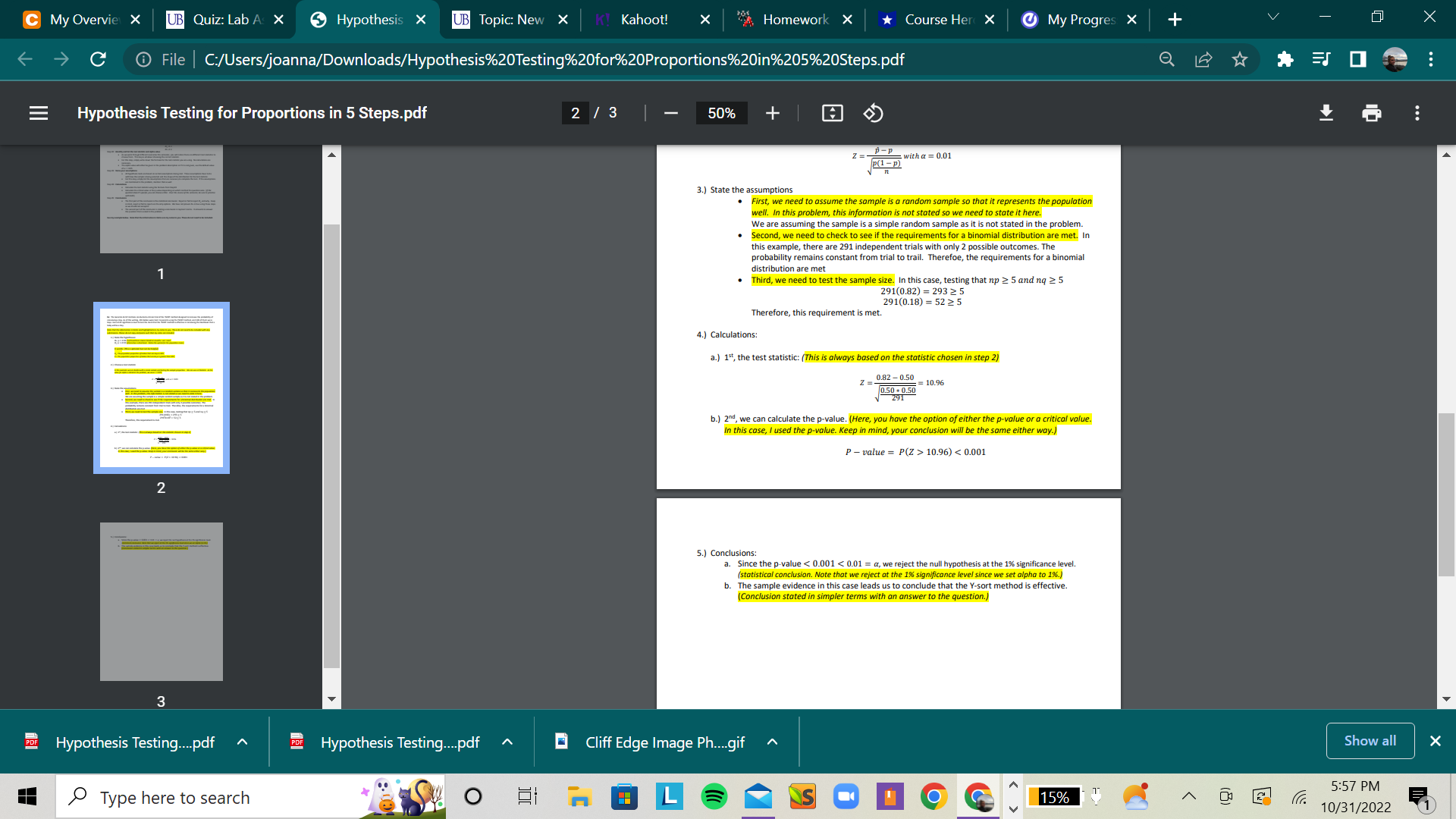
Hypothesis testing, Step 4 continued: Calculating the p-value. The Genetics & IVF Institute conducted a clinical trial of the YSORT method designed to increase the probability of conceiving a boy. As of this writing, 291 babies were born to parents using the YSORT method, and 239 of them were boys. Use a 0.01 significance level to test the claim that the YSORT method is effective in increasing the likelihood that a baby will be a boy.Using the Z-score from the previous question, calculate the p-value.
2: To find the P-value of the given test z = 10.96, while testing the claim that p > 0.5, follow the instructions below:
a) Press 2nd & DISTR & select "normalcdf( b) Enter the z value followed by 1000, 0,1 and press ENTER. The generated output is the requiredP-value.
Which of the following represents the range the p-value values in?
Group of answer choices
p-value >0.10
0.05 0.01 p-value Question 10 Hypothesis testing, Step 4 continued: Calculating the critical value. The Genetics & IVF Institute conducted a clinical trial of the YSORT method designed to increase the probability of conceiving a boy. As of this writing, 291 babies were born to parents using the YSORT method, and 239 of them were boys. Use a 0.01 significance level to test the claim that the YSORT method is effective in increasing the likelihood that a baby will be a boy. Findthecorrect critical value to test this claim 3: Tofind thecritical valuefollow the instructions below: a) Press 2nd & DISTR & select "invNorm( b) Enter the significance leveland press ENTER. The generated output is the critical value for a left-tailed test. Keep in mind this is a right tailed test.Note: If thesignificance level is not given, use 0.05. In this case, it is given as 0.01. Choose the correct critical value for this test, keeping in mind it is a right tailed test. Group of answer choices -2.326 2.326 Question 11 Hypothesis testing, Step 5: Drawing statistical conclusion. The Genetics & IVF Institute conducted a clinical trial of the YSORT method designed to increase the probability of conceiving a boy. As of this writing, 291 babies were born to parents using the YSORT method, and 239 of them were boys. Use a 0.01 significance level to test the claim that the YSORT method is effective in increasing the likelihood that a baby will be a boy.What conclusion can be drawn? The first way to draw a conclusion is to compare the critical value to the test statistic(Z-score). Fillin the blanks to draw a statistical conclusion here. Since the Z-score of [ Select ] ["10.96", "2.33"] is [ Select ] ["greater than", "less than"] the critical value of [ Select ] ["10.96", "2.33"] , we [ Select ] ["reject", "fail to reject"] the null hypothesis Question 12 Hypothesis testing, Step 5: Drawing statistical conclusion(cont). The Genetics & IVF Institute conducted a clinical trial of the YSORT method designed to increase the probability of conceiving a boy. As of this writing, 291 babies were born to parents using the YSORT method, and 239 of them were boys. Use a 0.01 significance level to test the claim that the YSORT method is effective in increasing the likelihood that a baby will be a boy.What conclusion can be drawn? The second way to draw a conclusion is to compare the p-value to the significance level. Fillin the blanks to draw a statistical conclusion here. Since the p-value is [ Select ] ["greater than", "less than", "equal to", ""] thesignificance level of [ Select ] ["0.01", "0.05"] , we [ Select ] ["reject", "fail to reject"] the null hypothesis Question 13 Hypothesis testing, Step 5: Layman's conclusion. The Genetics & IVF Institute conducted a clinical trial of the YSORT method designed to increase the probability of conceiving a boy. As of this writing, 291 babies were born to parents using the YSORT method, and 239 of them were boys. Use a 0.01 significance level to test the claim that the YSORT method is effective in increasing the likelihood that a baby will be a boy.What conclusion can be drawn? After drawing a statistical conclusion, we would put the conclusion into words for other's to follow. Fillin the blanks to draw a layman's conclusion here. The results of this study seem to indicate the the YSORT method is [ Select ] ["effective", "not effective.", "", ""] in increasing the likelihood that a boy will be a boy. Question 14 Nicotine Patches. In one study of smokers who tried to quit smoking with nicotine patch therapy, 39 were smoking one year after the treatment and 32 were not smoking one year after the treatment (based on data from "High-Dose Nicotine Patch Therapy," by Dale et al., Journal of the American Medical Association, Vol. 274, No, 17). Use a 0.05 significance level to test the claim that among smokers who try to quit with nicotine patch therapy, the majority are smoking a year after the treatment. What do these results suggest about the effectiveness of nicotine patch therapy for those trying to quit smoking? the 5 steps should match the steps in the example posted in the example here: Hypothesis Testing for Proportions in 5 Steps.pdfDownload Hypothesis Testing for Proportions in 5 Steps.pdf Use the first 13 questions of this lab as a guide. 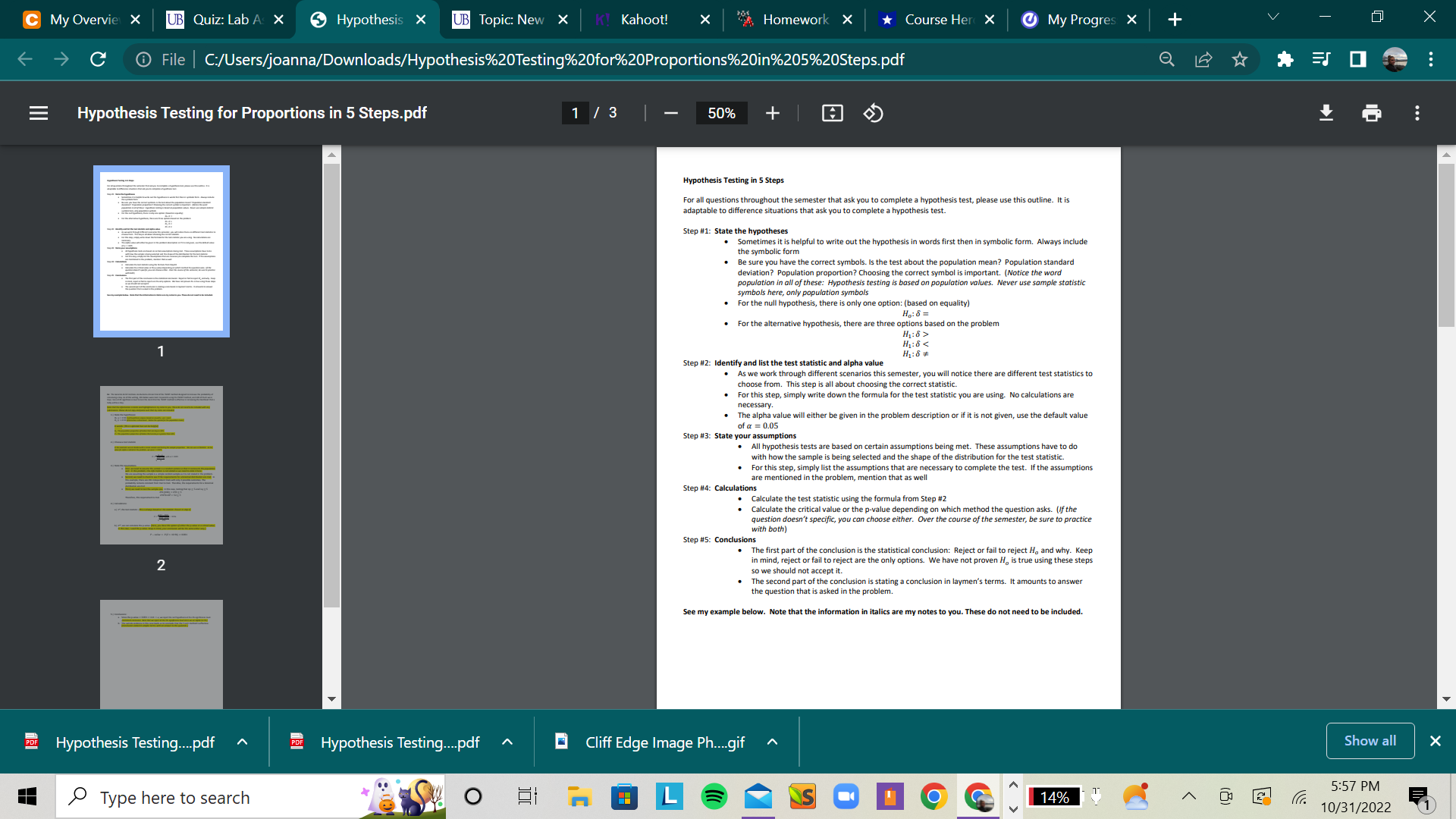
Step by Step Solution
There are 3 Steps involved in it
Step: 1

See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


