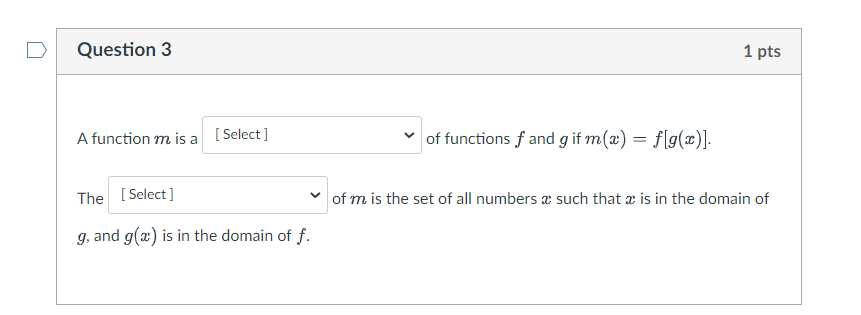
Question 1 Theorem: General Power Rule If u(x) is a differentiable function, n is any real number, and f(x) = [u(x)]", then O f'(x) = u(x)]" u'(x) O f'(x) = (n-1)[u(x)]"u'(x) O f'(x) = n[u(x)]"1 f'(x) = n[u(x)]* u'(x) O f'(x)=n[u'(x)]" u(x) Question 2 Theorem: The Chain Rule If m(x) = E[I(x)] is a composite function, then I'(x) exist. m' (x) = E' [I'(x)] Om'(x) = E[I(x)]I'(x) Om'(x) = E[I'(x)]I' (x) Om'(x) = E' [I(x)]I'(x) Om' (x) = E' [I'(x)]I'(x) , provided that E' [I(x)] and 1 pts 1 pts Question 3 1 pts A function m is a [Select] The [Select] g, and g(a) is in the domain of f. of functions f and g if m(x) = f(g(x)]. of m is the set of all numbers such that is in the domain of