Question
Question 10 : Now, we would like to explore the impact of having less samples in the signal which also means less samples available for
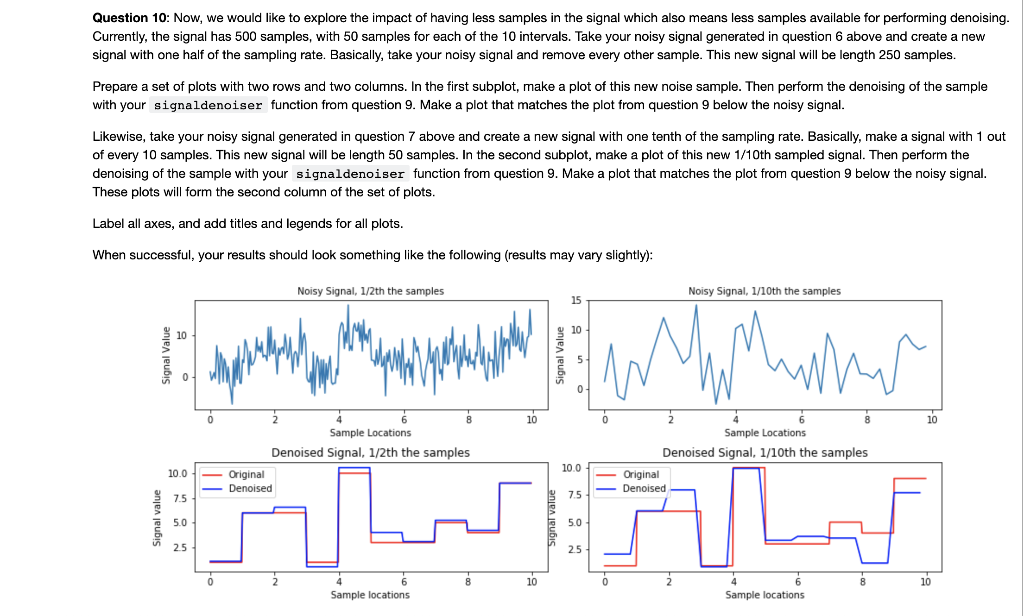
Question 10: Now, we would like to explore the impact of having less samples in the signal which also means less samples available for performing denoising. Currently, the signal has 500 samples, with 50 samples for each of the 10 intervals. Take your noisy signal generated in question 6 above and create a new signal with one half of the sampling rate. Basically, take your noisy signal and remove every other sample. This new signal will be length 250 samples.
Prepare a set of plots with two rows and two columns. In the first subplot, make a plot of this new noise sample. Then perform the denoising of the sample with your signaldenoiser function from question 9. Make a plot that matches the plot from question 9 below the noisy signal.
Likewise, take your noisy signal generated in question 7 above and create a new signal with one tenth of the sampling rate. Basically, make a signal with 1 out of every 10 samples. This new signal will be length 50 samples. In the second subplot, make a plot of this new 1/10th sampled signal. Then perform the denoising of the sample with your signaldenoiser function from question 9. Make a plot that matches the plot from question 9 below the noisy signal. These plots will form the second column of the set of plots.
Label all axes, and add titles and legends for all plots.
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


