Question 15 Thx! 


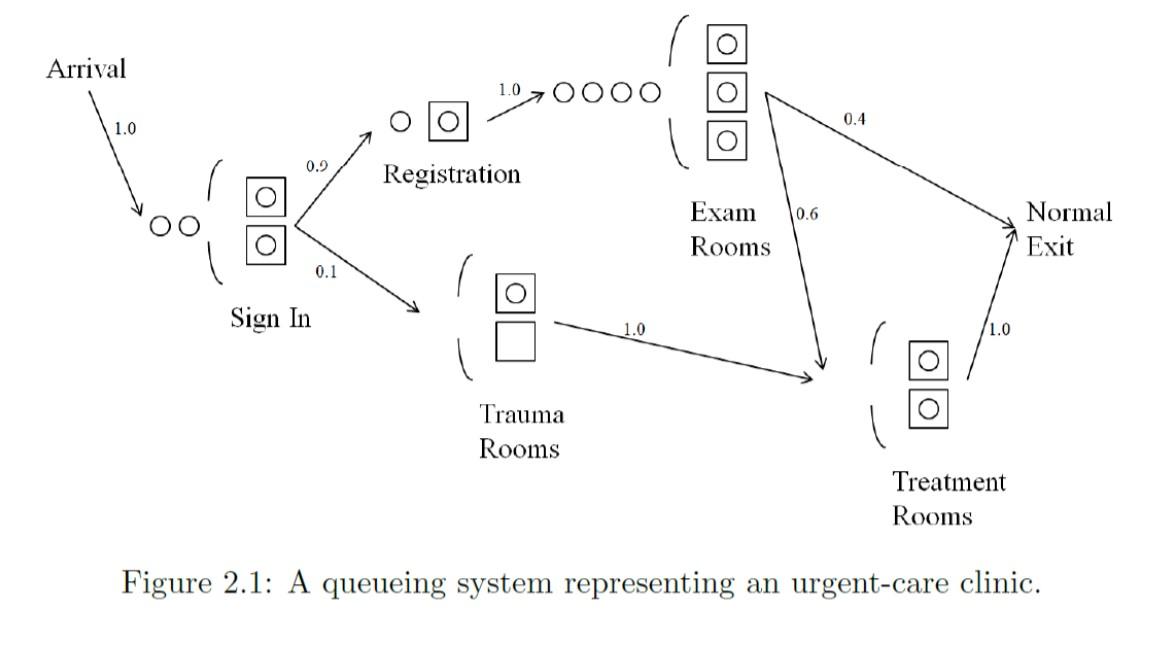
15. In Problems 12 and 13 (and without the extra resource unit), the budget's been cut and we need to eliminate one of the ten individual servers across the clinic; however, we have to keep at least one at each station. Where would this cut be least damaging to the system's operation? Could we cut two servers and expect the system still to "work?" More than two? 12. In the urgent-care clinic of Figure 2.1, suppose that the patients arrive from outside into the clinic (coming from the upper right corner of the figure and always into the Sign In station) with interarrival times that are exponentially distributed with mean 6 minutes. The number of individual servers at each station and the branching probabilities are all as shown in Figure 2.1. The service times at each node are exponentially distributed with means (all in minutes) of 3 for Sign In, 5 for Registration, 90 for Trauma Rooms, 16 for Exam Rooms, and 15 for Treatment Rooms. For each of the five stations, compute the "local" traffic intensity Station there. Will this clinic "work," i.e., be able to handle the external patient load? Why or why not? If you could add a single server to the system, and add it to any of the five stations, where would you add it? Why? 3. In Problem 12, for each of the five stations, compute each of Wq,W, Lq,L, and , and interpret in words. Would you still make the same decision about where to add that extra single resource unit that you did in Problem 12? Why or why not? (Remember these are sick people, some of them seriously ill, not widgets being pushed through a factory.) Hint: Figure 2.1: A queueing system representing an urgent-care clinic. 15. In Problems 12 and 13 (and without the extra resource unit), the budget's been cut and we need to eliminate one of the ten individual servers across the clinic; however, we have to keep at least one at each station. Where would this cut be least damaging to the system's operation? Could we cut two servers and expect the system still to "work?" More than two? 12. In the urgent-care clinic of Figure 2.1, suppose that the patients arrive from outside into the clinic (coming from the upper right corner of the figure and always into the Sign In station) with interarrival times that are exponentially distributed with mean 6 minutes. The number of individual servers at each station and the branching probabilities are all as shown in Figure 2.1. The service times at each node are exponentially distributed with means (all in minutes) of 3 for Sign In, 5 for Registration, 90 for Trauma Rooms, 16 for Exam Rooms, and 15 for Treatment Rooms. For each of the five stations, compute the "local" traffic intensity Station there. Will this clinic "work," i.e., be able to handle the external patient load? Why or why not? If you could add a single server to the system, and add it to any of the five stations, where would you add it? Why? 3. In Problem 12, for each of the five stations, compute each of Wq,W, Lq,L, and , and interpret in words. Would you still make the same decision about where to add that extra single resource unit that you did in Problem 12? Why or why not? (Remember these are sick people, some of them seriously ill, not widgets being pushed through a factory.) Hint: Figure 2.1: A queueing system representing an urgent-care clinic










