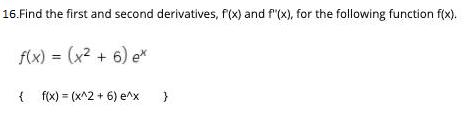
16.Find the first and second derivatives, f(x) and f"(x), for the following function f(x). f(x) = (x2 + 6) e* { f(x) = (x^2 + 6) e^x QUESTION 17 Second derivative with quotient rule Find the first and second derivatives, g'(x) and g"(x), for the fuction g(x) given as follows sin x g(x) g(x) = [ (sin x) / (x) 1 QUESTION 18 Position, Velocity, Acceleration Trigonometric (also requires basic chain rule: (d/dt) sin (wt) = w cos (wt) ) Expanding ideas of # 11 add frequency, phase shift R(t) = A cos (wt + p) { R(t) = A cos (wt + p) } Amplitude A frequency w phase shift p/w Consider the following example of harmonic motion R(t) = 5 cos (2t) R(t) = 5 cos (2 t) } a) Find both the velocity v(t) = r'(t) and the acceleration a(t) = v'(t) = r"(t) b) Observe the relation between the acceleration a(t) and the position r(t). (in diff ean) QUESTION 19 Higher derivatives a) Find the first 3 derivatives of f(x) given as follows f(x) = x2 e* %3D { f(x) = x^2 e^x b) Find the first 4 derivatives of g(x) given as follows g(x) = x cos x { g(x) = x cos x } C) Find the first 4 derivatives of f(x) given as follows why are all remaining higher derivatives 0? f(x) = 2x4 + 3x? - 8x + 5 %3D QUESTION 20 second derivative and concavity Consider the function f(x) defined as follows f(x) x3 + 3x2 %3D { f(x) = x^3 + 3x^2 } a) Find the first and second derivative f(x) and f"(x). Observe that f"(x) > 0 on the interval (-1, infinity). b) Evaluate f(a) for the following values of a: a = -1, 1, 3 Observe that the slope of the tangent line increases as we move (Why is this what would be expected when the f'"(x) = rate of change of f(x) is positive on this region?} c) Consider what this increase in the slope of the tangent line on this interval means for the shape of the graph. Sketch the graph and include the tangent lines at (a, f(a)) for a = -1, 1, 3. Observe why the increase in slope implies the curve will bend above the tangent line.