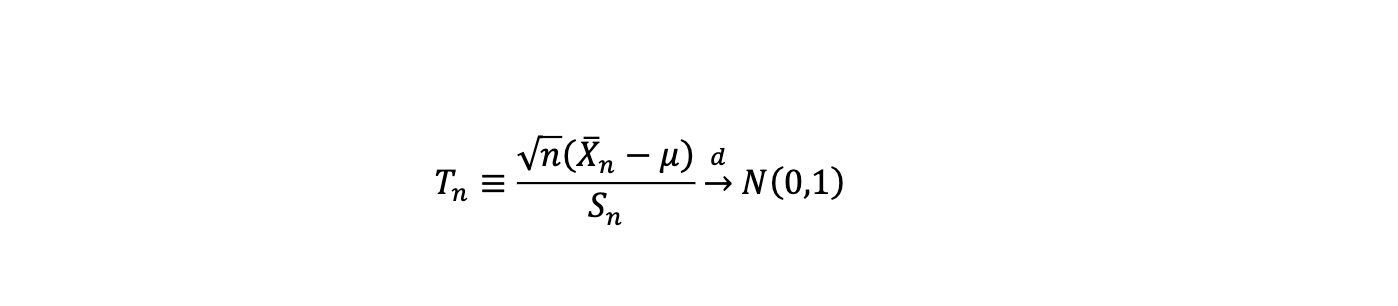
Question 2 (20 points) n Let X, ..., X be i.i.d. random variables from some distribution with E(X) = and Var(X;) = < , and E(X?) < . Let 1 == n n i=1 Xi n 1 S2 = and n- - (XX - Xn) be the sample mean and sample variance. i=1 (a) (3) What does the weak law of large numbers say about X? (b) (3) What does the central limit theorem say about Xn? (c) (8) Let S Show $20. > = n n n (x - Xn) = =- == > xx - X i=1 i=1 [Hint: Consider the limiting behaviour of U = = X and V = X and use the P fact that Un u, Vn P n v implies Un + Vn uv]. (d) (6) Using the conclusion drawn in (c), show S2 and hence show that n(xn-) a Tn = Sn d N (0,1)