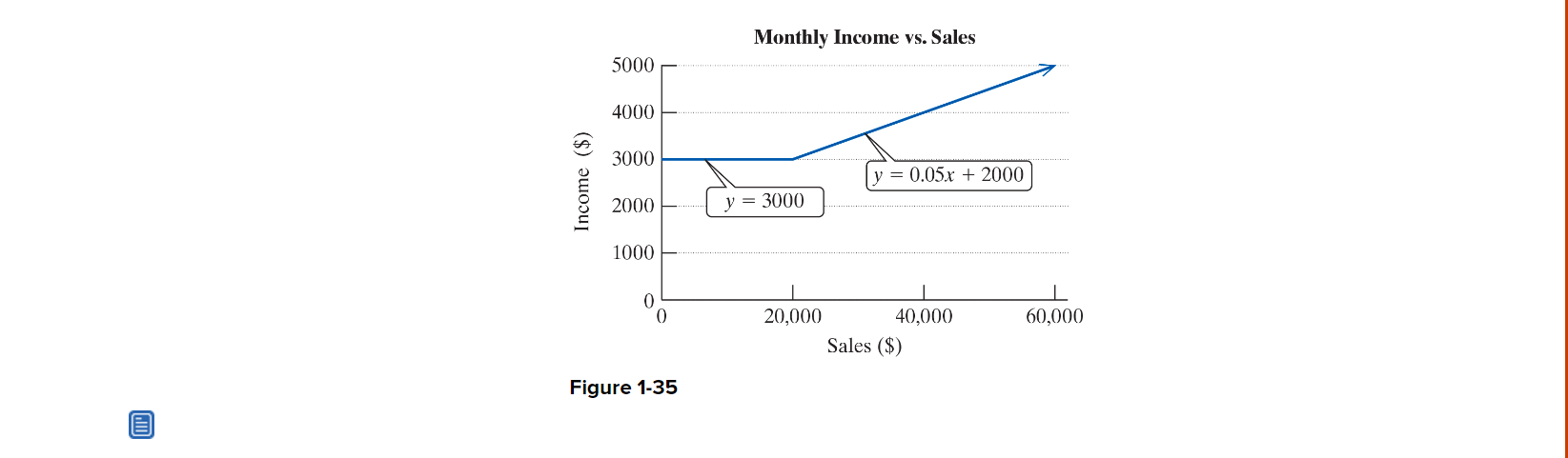
Question 2: Create. (a) Create your own piecewise-defined function to model a real-life situation such as your commute, a monthly salary (example #9, and problem #87 on page 212) or a cell phone plan (problem #88 page 212). State the function's equation and give a description of the function stating the input and output of your function. (6 pts) (b) Sketch an accurate graph of your newly-created function using appropriate axes values. (Note that in some cases it's appropriate to use non-integer values for the independent variable.) Include values where the function changes. (4 pts) (c) Evaluate the piecewise function at three values and interpret what these points represent in the context of your problem. (6 pts) (d) Identify the domain and range appropriate for your problem situation. Write your answers using set-builder notation. (4 pts) (e) State where the function is increasing, decreasing or constant using interval notation. (section 1.7 page 205) (4 pts.) EXAMPLE 9 Using a Piecewise-Defined Function in an Application A salesperson makes a monthly salary of $3000 along with a 5% commission on sales over $20,000 for the month. Write a piecewise-defined function to represent the salesperson's monthly income I (x) (in $) for x dollars in sales. Solution: Let x represent the amount in sales. Then x - 20,000 represents the amount in sales over $20,000. There are two scenarios for the salesperson's income. Scenario 1: The salesperson sells $20,000 or less. In this case, the monthly income is a constant $3000. This is represented by y = 3000 for 0 x 20,000 Scenario 2: The salesperson sells over $20,000. In this case, the monthly income is $3000 plus 5% of sales over $20,000. This is represented by y=3000+ 0.05 (x - 20,000) for x > 20,000 Therefore, a piecewise-defined function for monthly income is 1(x) = {. 3000 3000+ 0.05 (x - 20,000) for 0 x20,000 for x > 20,000 Alternatively, we can simplify to get 1(x)= = { 3000 for 0x20,000 0.05x + 2000 for x > 20,000 A graph of y = (x) is shown in Figure 1-35. Notice that for x = $20,000, both equations within the piecewise-defined function yield a monthly salary of $3000. Therefore, the two line segments in the graph meet at (20,000, 3000). Page 205 Income ($) 5000 4000 Monthly Income vs. Sales 3000 y = 0.05x + 2000 2000 y = 3000 1000 0 20,000 40,000 60,000 Sales ($) Figure 1-35 87. A salesperson makes a base salary of $2000 per month. Once he reaches $40,000 in total sales, he earns an additional 5% commission on the amount in sales over $40,000. Write a piecewise-defined function to model the salesperson's total monthly salary $ (x) (in $) as a function of the amount in sales x. Answer