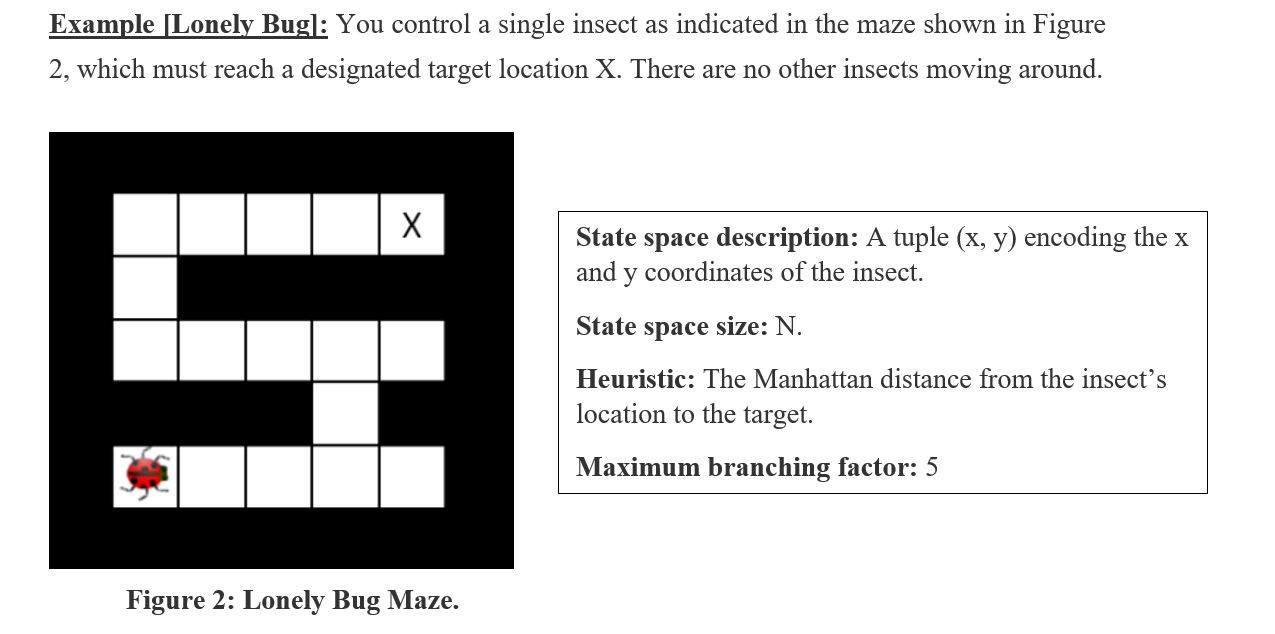
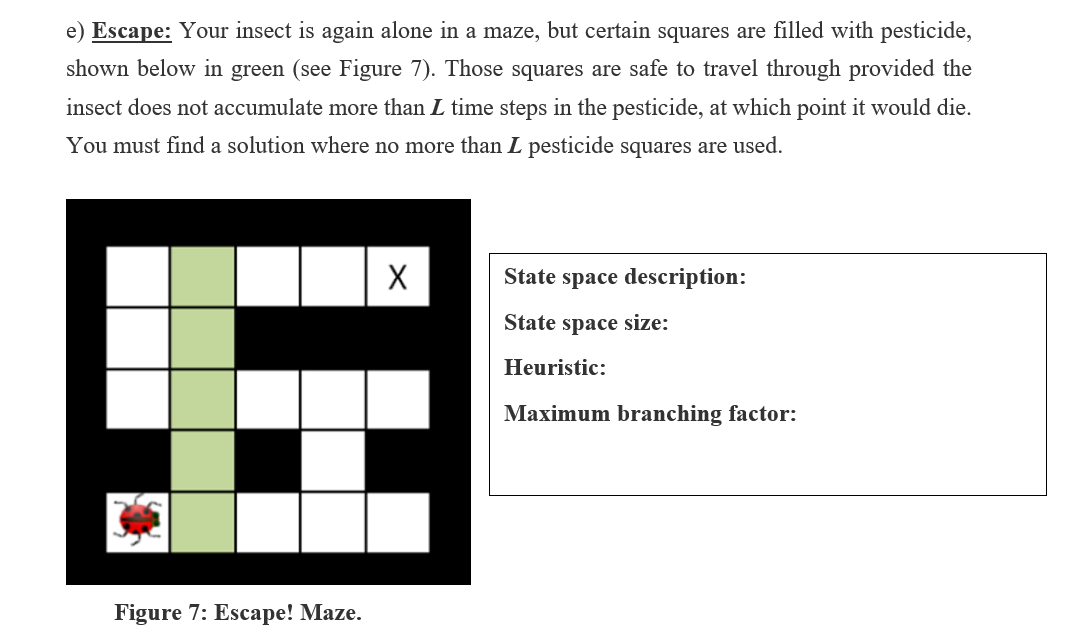
Question 2 Hive Minds You control one or more insects in a rectangular maze-like environment. At each time step, an insect can move into an adjacent square if that square is currently free, or the insect may stay in its current lo cation. In the case of multiple insects adjacent insects cannot swap lo cations Squares may be blocked by walls. There are N non-wall squares. Optimality is always in terms of time steps; all actions have cost 1 regardless of the number of insects moving or where they move. For each of the following scenarios, precisely but compactly define the state space and give its size. Then, give a non-trivial admissible heuristic for the problem and the maximum branching factor. Your answers should follow the format in the example case below. Full credit requires a minimal state space (i.e. do not include extra information) and a reasonable non- trivial heuristic. The heuristic must be admissible, but you are not required to prove admissibility. The illustrations are given as examples; your answers should not assume a speciiic maze. Example [Lonely Bugl: You control a single insect as indicated in the maze shown in Figure 2, which must reach a designated target location X. There are no other insects moving around. State space description: A tuple (x, y) encoding the x and y coordinates of the insect. State space size: N Heuristic: The Manhattan distance from the insect's location to the target. Maximum branching factor: 5 Figure 2: Lonely Bug Maze. c) Step On It: Your single insect is alone in the maze again. This time, it can speed up as. long as it does not change direction. Specifically, after a move of v squares in some direction, it can move up to v + I squares in that same direction on the next time step. It can move fewer than v+I squares in that direction, as well, and it can move one square in any other direction (or stand still). Moving v squares requires that all intermediate squares passed over, as well as the v-th square, currently be empty. The cost of a multi-square move is still 1 time unit. Let L be the size of the longest straight corridor in the maze. In the example below (see Figure 5), L 7 and the dots in the maze below indicate where the insect will be after each time step in the optimal (fewest time step) plan: State space description: State space size: Heuristic: Maximum branching factor: Figure 5: Step on It Maze (L7) d) Lost at Night: It is night and you control a single insect. You know the maze, but you do not know what square the insect will start in. Let M be the set of non-wall squares in the maze, i.e. M- N. You must pose a search problem whose solution is an all-purpose sequence of actions such that, after executing those actions, the insect will be on the exit square, regardless of initial position. The insect executes the actions mindlessly and does not know whether its moves succeed: if it uses an action which would move it in a blocked direction, it will stay where it is. For example, in the maze shown in Figure 6, moving left twice and then right twice guarantees that the insect will be at the exit regardless of its starting position. State space description: State space size: Heuristic: Maximum branching factor: Figure 6: Lost At Night Maze. e) Escape: Your insect is again alone in a maze, but certain squares are filled with pesticide, shown below in green (see Figure 7). Those squares are safe to travel through provided the insect does not accumulate more than L time steps in the pesticide, at which point it would die You must find a solution where no more than L pesticide squares are used. State space description: State space size: Heuristic: Maxi imum branching factor: Figure 7: Escape! Maze. Question 2 Hive Minds You control one or more insects in a rectangular maze-like environment. At each time step, an insect can move into an adjacent square if that square is currently free, or the insect may stay in its current lo cation. In the case of multiple insects adjacent insects cannot swap lo cations Squares may be blocked by walls. There are N non-wall squares. Optimality is always in terms of time steps; all actions have cost 1 regardless of the number of insects moving or where they move. For each of the following scenarios, precisely but compactly define the state space and give its size. Then, give a non-trivial admissible heuristic for the problem and the maximum branching factor. Your answers should follow the format in the example case below. Full credit requires a minimal state space (i.e. do not include extra information) and a reasonable non- trivial heuristic. The heuristic must be admissible, but you are not required to prove admissibility. The illustrations are given as examples; your answers should not assume a speciiic maze. Example [Lonely Bugl: You control a single insect as indicated in the maze shown in Figure 2, which must reach a designated target location X. There are no other insects moving around. State space description: A tuple (x, y) encoding the x and y coordinates of the insect. State space size: N Heuristic: The Manhattan distance from the insect's location to the target. Maximum branching factor: 5 Figure 2: Lonely Bug Maze. c) Step On It: Your single insect is alone in the maze again. This time, it can speed up as. long as it does not change direction. Specifically, after a move of v squares in some direction, it can move up to v + I squares in that same direction on the next time step. It can move fewer than v+I squares in that direction, as well, and it can move one square in any other direction (or stand still). Moving v squares requires that all intermediate squares passed over, as well as the v-th square, currently be empty. The cost of a multi-square move is still 1 time unit. Let L be the size of the longest straight corridor in the maze. In the example below (see Figure 5), L 7 and the dots in the maze below indicate where the insect will be after each time step in the optimal (fewest time step) plan: State space description: State space size: Heuristic: Maximum branching factor: Figure 5: Step on It Maze (L7) d) Lost at Night: It is night and you control a single insect. You know the maze, but you do not know what square the insect will start in. Let M be the set of non-wall squares in the maze, i.e. M- N. You must pose a search problem whose solution is an all-purpose sequence of actions such that, after executing those actions, the insect will be on the exit square, regardless of initial position. The insect executes the actions mindlessly and does not know whether its moves succeed: if it uses an action which would move it in a blocked direction, it will stay where it is. For example, in the maze shown in Figure 6, moving left twice and then right twice guarantees that the insect will be at the exit regardless of its starting position. State space description: State space size: Heuristic: Maximum branching factor: Figure 6: Lost At Night Maze. e) Escape: Your insect is again alone in a maze, but certain squares are filled with pesticide, shown below in green (see Figure 7). Those squares are safe to travel through provided the insect does not accumulate more than L time steps in the pesticide, at which point it would die You must find a solution where no more than L pesticide squares are used. State space description: State space size: Heuristic: Maxi imum branching factor: Figure 7: Escape! Maze