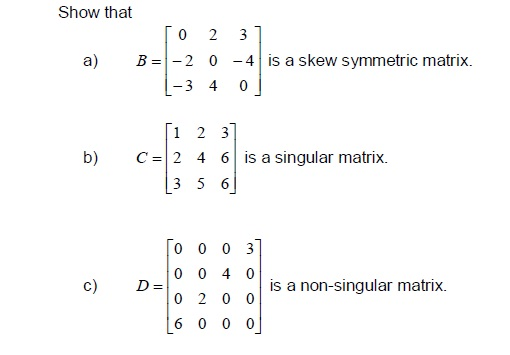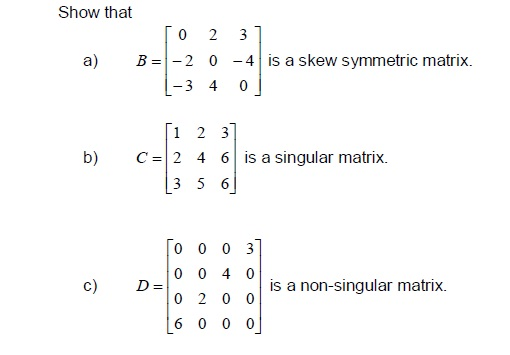
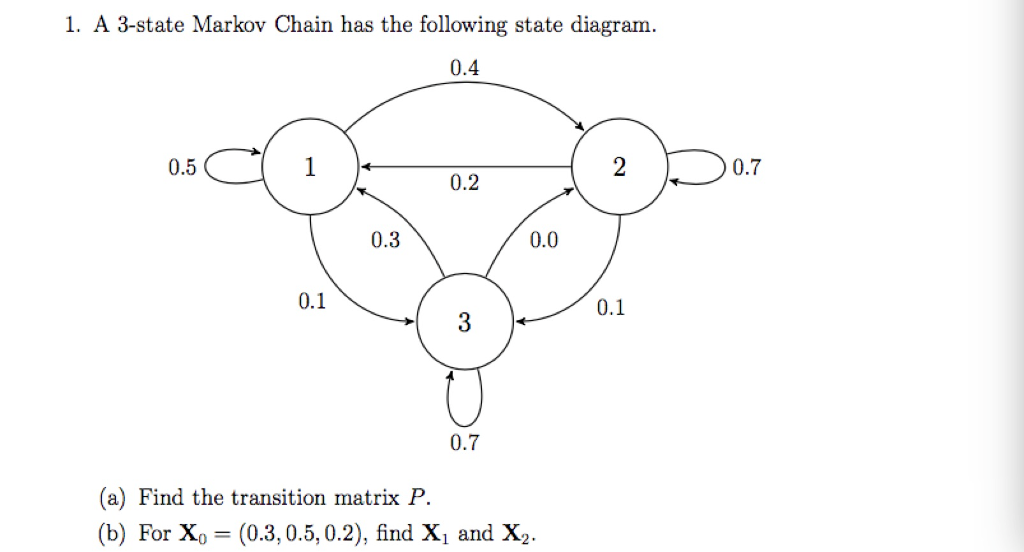
Question:
2.4: An oil prospector will drill a succession of holes in a given area to find a productive well. The probability that he is successful on a given trial is 0.3.
2.4.1 Use both the Geometric and Negative Binomial probability distribution functions to calculate the probability that the third hole drilled is the first to yield a productive well? (3)
2.4.2 If the prospector can afford to drill at most ten wells, what is the probability that he will fail to find a productive well? Use the Binomial and Geometric distributions to calculate the probability and appropriately interpret your answer.
2.5 We observe a sequence of independent identical trials with two possible outcomes on
each trial, ?? and ??, and with ??(??) = ??. The number of the trial on which we observe the fifth success, ?? has a negative binomial distribution with parameters ?? = 7 and ??. Suppose that we observe the fifth success on trial number 12.
2.5.1 Find the value of p that maximizes ??(?? = 12).
2.5.2 Generalize the result from part (2.5.1) to find the value of ?? that maximizes
??(?? = ??0) when ?? has a negative binomial distribution with parameters ?? (known) and ??.
Please answer question A and B by reading the central limit theorem below .A. Why is the central limit theorem important? Answer. B. What is wrong with and missing from the following statement of the central limit theorem? Central Limit Theorem. ' If the random variables X1, X2, X3... ., Xn are a random sample of size n\" from anyr distribution with nite mean u and variance 02, then the distribution of X}? will be approximately normal, with a standard deviation of (I! ml'r.' Which of the following statements are TRUE regarding Central Limit Theorem? CCS The central limit theorem gives the exact probability of estimating the true population mean. Chart / Roll The central limit theorem only applies when the population distribution is normal. The range of values for the sampling distribution of means is larger than the range of values in the population. The central limit theorem requires that all samples are randomly selected from a single population.For the following word problems state if the problem requires using the Central Limit theorem or if does Not require using the Central limit theorem Circle the correct choice: 1. What is the probability of randomly selecting an adult with an IQ score less than 75? A. Requires the Central limit theorem. B. Does not require the central limit theorem. 2. If 30 cell phones are randomly selected what is the probability the cell phones will last an average of more than 23.8 months? A. Requires the Central limit theorem. B. Does not require the central limit theorem. 3. In general Marine platoons are around 50 strong, if a sample of a given platoon is taken from a populati of Marines with a mean weight of 200 pounds and with standard deviation o = 10. What is the probabil that the sample mean weight will be less than 196 pounds? A. Requires the Central limit theorem. B. Does not require the central limit theorem. 4. The mean age of baseball players is 27 years. Assuming the age of baseball players are normally distributed and that the average size of a baseball team is 25 players, what is the probability a basebal player is older than 30 years if the player is randomly selected. A. Requires the Central limit theorem. B. Does not require the central limit theorem. 5. Suppose that you have a sample of 81 students from a population with mean u = 500 and with standard deviation o = 108. What is the probability that the sample mean will be greater than 483. A. Requires the Central limit theorem. B. Does not require the central limit theorem.Show that 0 37 a) B = -2 0 -4 is a skew symmetric matrix. -3 4 0 12 3 b) C = 2 4 6 is a singular matrix. 13 5 6 0 0 0 3 0 0 4 0 C) D = is a non-singular matrix. 0 2 0 0 6 0 0 01. A 3-state Markov Chain has the following state diagram. 0.4 0.5 N 0.7 0.2 0.3 0.0 0.1 0.1 3 0.7 (a) Find the transition matrix P. (b) For Xo = (0.3, 0.5, 0.2), find X1 and X2