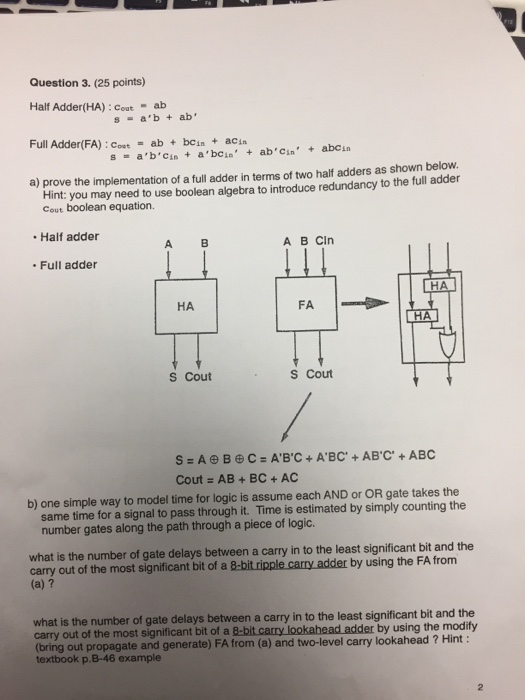
Question 3. (25 points) Half Adder(HA) : Cout ab s a b ab' Full Adder(FA) : Coat = ab + bcin + acin a,b,cin a,bCin, ab 'cin' + abcin s = + + a) prove the implementation of a full adder in terms of two half adders as shown below Hint: you may need to use boolean algebra to introduce redundancy to the full adder Cout boolean equation. Half adder Full adder A B Cin HA HA FA S Cout S Cout Cout = AB + BC + AC b) one simple way to model time for logic is assume each AND or OR gate takes the same time for a signal to pass through it. Time is estimated by simply counting the number gates along the path through a piece of logic. what is the number of gate delays between a carry in to the least significant bit and the carry out of the most significant bit of a 8-bit ripple carry adder by using the FA from (a) ? what is the number of gate delays between a carry in to the least significant bit and the carry out of the most significant bit of a 8-bit carry lookahead adder by using the (bring out propagate and generate) FA from (a) and two-level carry lookahead ? Hint: textbook p.B-46 example modity Question 3. (25 points) Half Adder(HA) : Cout ab s a b ab' Full Adder(FA) : Coat = ab + bcin + acin a,b,cin a,bCin, ab 'cin' + abcin s = + + a) prove the implementation of a full adder in terms of two half adders as shown below Hint: you may need to use boolean algebra to introduce redundancy to the full adder Cout boolean equation. Half adder Full adder A B Cin HA HA FA S Cout S Cout Cout = AB + BC + AC b) one simple way to model time for logic is assume each AND or OR gate takes the same time for a signal to pass through it. Time is estimated by simply counting the number gates along the path through a piece of logic. what is the number of gate delays between a carry in to the least significant bit and the carry out of the most significant bit of a 8-bit ripple carry adder by using the FA from (a) ? what is the number of gate delays between a carry in to the least significant bit and the carry out of the most significant bit of a 8-bit carry lookahead adder by using the (bring out propagate and generate) FA from (a) and two-level carry lookahead ? Hint: textbook p.B-46 example modity