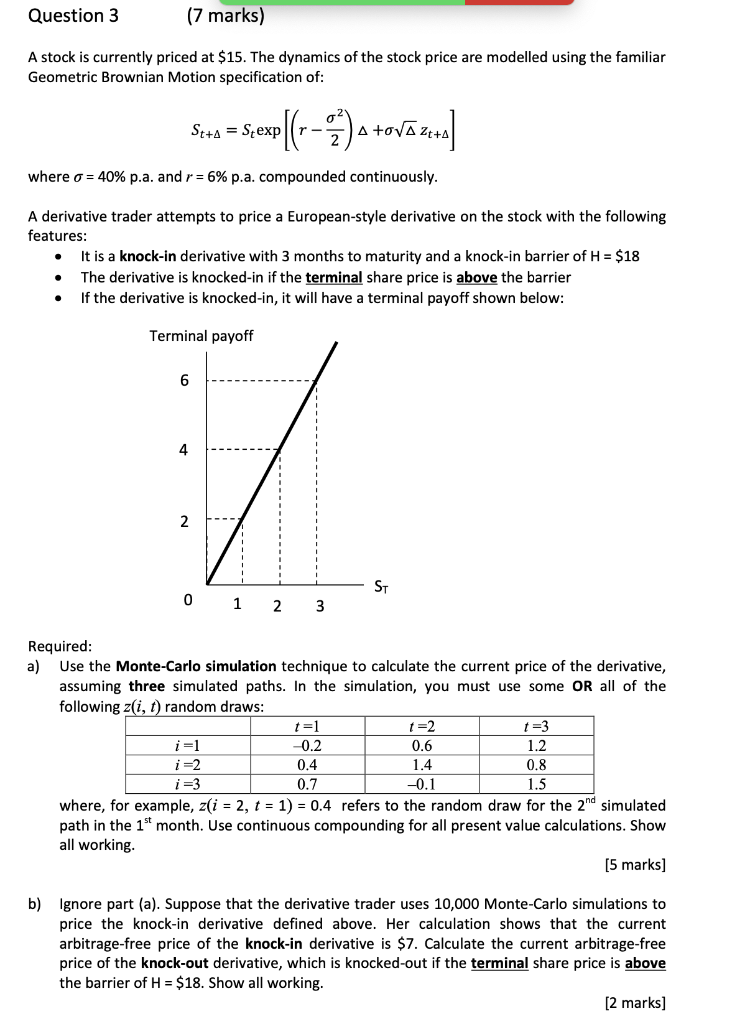
Question 3 (7 marks) A stock is currently priced at $15. The dynamics of the stock price are modelled using the familiar Geometric Brownian Motion specification of: St+A = - Seve||--->) a tovo za p( A where o = 40% p.a. and r = 6% p.a. compounded continuously. A derivative trader attempts to price a European-style derivative on the stock with the following features: It is a knock-in derivative with 3 months to maturity and a knock-in barrier of H = $18 The derivative is knocked-in if the terminal share price is above the barrier If the derivative is knocked-in, it will have a terminal payoff shown below: . . Terminal payoff 6 4 7 2 ST 0 1 2 3 Required: a) Use the Monte-Carlo simulation technique to calculate the current price of the derivative, assuming three simulated paths. In the simulation, you must use some OR all of the following zi, t) random draws: t=1 t=2 t=3 i=1 0.2 0.6 1.2 i=2 0.4 1.4 0.8 i=3 0.7 -0.1 1.5 where, for example, z(i = 2, t = 1) = 0.4 refers to the random draw for the 2nd simulated path in the 1st month. Use continuous compounding for all present value calculations. Show all working. [5 marks) b) Ignore part (a). Suppose that the derivative trader uses 10,000 Monte-Carlo simulations to price the knock-in derivative defined above. Her calculation shows that the current arbitrage-free price of the knock-in derivative is $7. Calculate the current arbitrage-free price of the knock-out derivative, which is knocked-out if the terminal share price is above the barrier of H = $18. Show all working. [2 marks] Question 3 (7 marks) A stock is currently priced at $15. The dynamics of the stock price are modelled using the familiar Geometric Brownian Motion specification of: St+A = - Seve||--->) a tovo za p( A where o = 40% p.a. and r = 6% p.a. compounded continuously. A derivative trader attempts to price a European-style derivative on the stock with the following features: It is a knock-in derivative with 3 months to maturity and a knock-in barrier of H = $18 The derivative is knocked-in if the terminal share price is above the barrier If the derivative is knocked-in, it will have a terminal payoff shown below: . . Terminal payoff 6 4 7 2 ST 0 1 2 3 Required: a) Use the Monte-Carlo simulation technique to calculate the current price of the derivative, assuming three simulated paths. In the simulation, you must use some OR all of the following zi, t) random draws: t=1 t=2 t=3 i=1 0.2 0.6 1.2 i=2 0.4 1.4 0.8 i=3 0.7 -0.1 1.5 where, for example, z(i = 2, t = 1) = 0.4 refers to the random draw for the 2nd simulated path in the 1st month. Use continuous compounding for all present value calculations. Show all working. [5 marks) b) Ignore part (a). Suppose that the derivative trader uses 10,000 Monte-Carlo simulations to price the knock-in derivative defined above. Her calculation shows that the current arbitrage-free price of the knock-in derivative is $7. Calculate the current arbitrage-free price of the knock-out derivative, which is knocked-out if the terminal share price is above the barrier of H = $18. Show all working. [2 marks]







