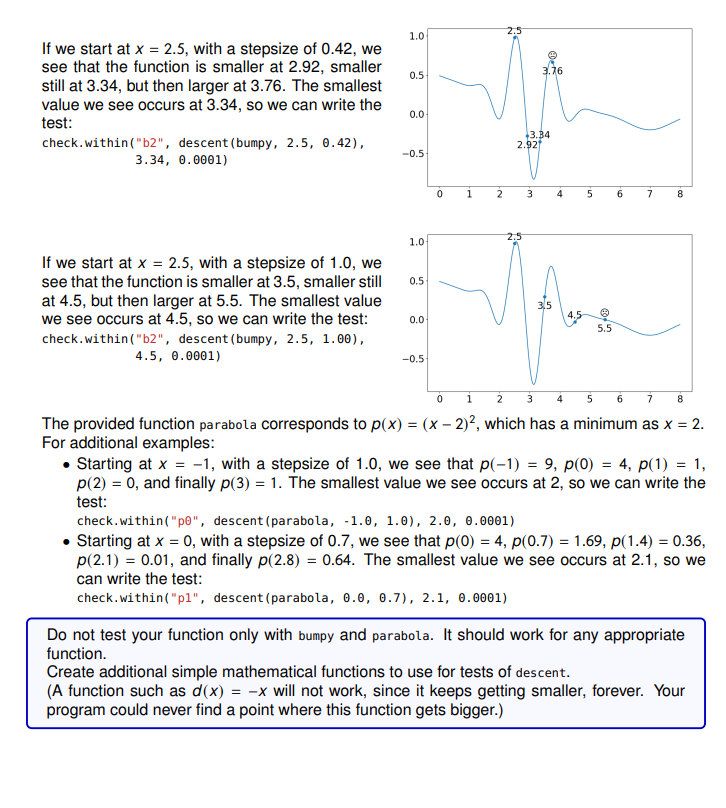
Question 3: Descent Write a function descent (f: callable, x0: float, stepsize: float) -> float. Starting at xe, it examines the value of f at all values spaced apart by stepsize, as long as the values continue to get smaller. It returns the x last value checked before the function started getting larger. Exercise We will see examples using the function bumpy, provided in the start code. It looks like this: 1.0- 0.5 0.0 -0.5 0 1 ter 2 3 h 4 If we start at x = 5, with a stepsize of 1, we see that the function is smaller at 6, and still smaller at 7, but then larger at 8. The smallest value we see occurs at 7, so we can write the test: check. within ("b0", descent (bumpy, 5.0, 1.0), 7.0, 0.0001) check.within ("b1", descent (bumpy, 5.0, 0.42), 7.1, 0.0001) If we start at x = 5, with a stepsize of 0.42, we see that the function is smaller at 5.42, smaller still at 5.84, 6.26, 6.68, and 7.1, but then larger at 7.52. The smallest value we see occurs at 7.1, so we can write the test: Fin 1.0 0.5 0.0 -0.5 1.0 0.5 0.0 -0.5 10 6 0 0 7 1 1 8 2 2 3 w 3 5.0 4 5 5.0 6.0 4 5 6 5.84 5.42 6.26 6 7.0 8.0 7 8 6.68 7.52 7.19 7 8 If we start at x = 2.5, with a stepsize of 0.42, we see that the function is smaller at 2.92, smaller still at 3.34, but then larger at 3.76. The smallest value we see occurs at 3.34, so we can write the test: check.within ("b2", descent (bumpy, 2.5, 0.42), 3.34, 0.0001) If we start at x = 2.5, with a stepsize of 1.0, we see that the function is smaller at 3.5, smaller still at 4.5, but then larger at 5.5. The smallest value we see occurs at 4.5, so we can write the test: check.within ("b2", descent (bumpy, 2.5, 1.00), 4.5, 0.0001) 1.0 0.5- 0.0 -0.5 1.0 0.5 0.0 -0.5 0 1 2 2.5 43.34 2.92 2.5 3.76 3 3,5 4 5 5.5 7 8 0 1 2 3 4 5 6 7 8 The provided function parabola corresponds to p(x) = (x - 2), which has a minimum as x = 2. For additional examples: Starting at x = -1, with a stepsize of 1.0, we see that p(-1) = 9, p(0) = 4, p(1) = 1, p(2) = 0, and finally p(3) = 1. The smallest value we see occurs at 2, so we can write the test: check. within ("P0", descent (parabola, -1.0, 1.0), 2.0, 0.0001) Starting at x = 0, with a stepsize of 0.7, we see that p(0) = 4, p(0.7) = 1.69, p(1.4) = 0.36, p(2.1) = 0.01, and finally p(2.8) = 0.64. The smallest value we see occurs at 2.1, so we can write the test: check.within("p1", descent (parabola, 0.0, 0.7), 2.1, 0.0001) Do not test your function only with bumpy and parabola. It should work for any appropriate function. Create additional simple mathematical functions to use for tests of descent. (A function such as d(x) = -x will not work, since it keeps getting smaller, forever. Your program could never find a point where this function gets bigger.)