Question
Question 3 For each of the modal arguments below, show that they are invalid by providing a counterexample. Show the invalidity of the modal argument
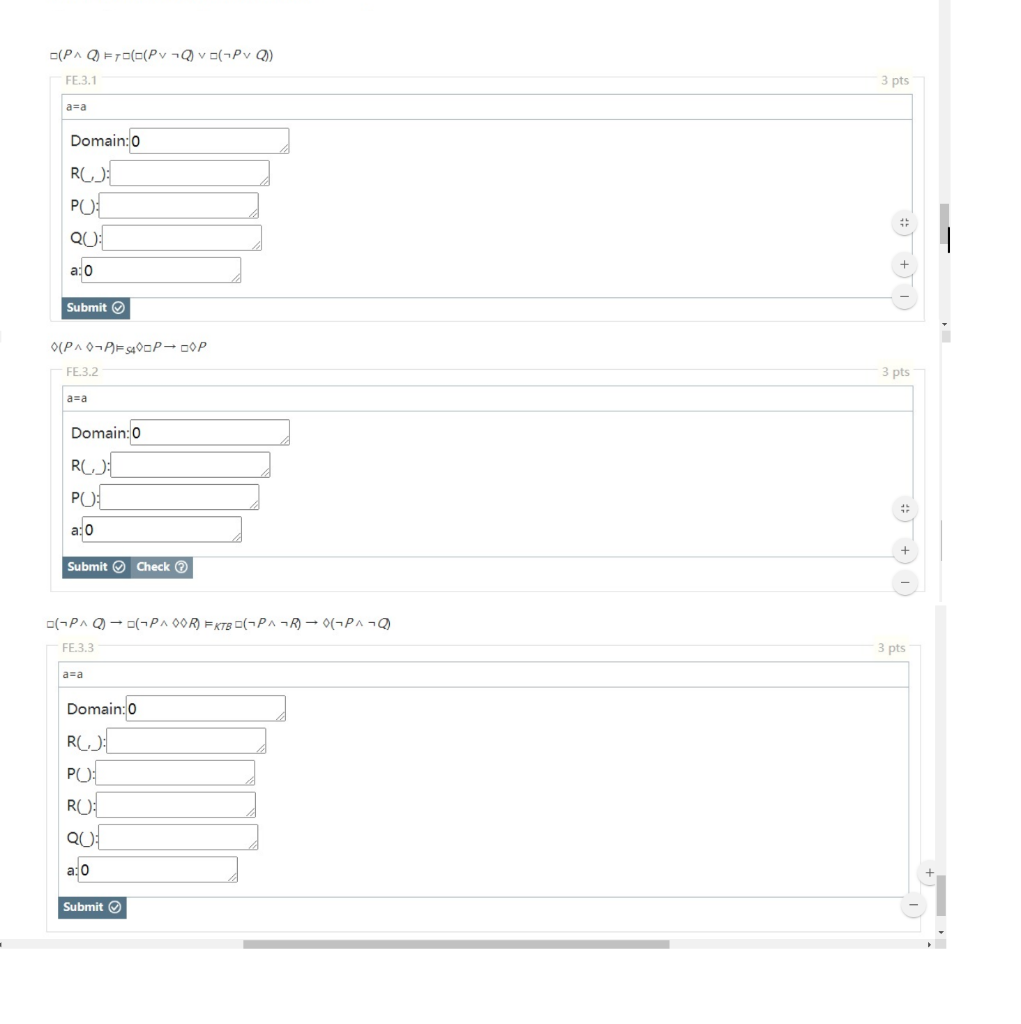
Question 3
For each of the modal arguments below, show that they are invalid by providing a counterexample. Show the invalidity of the modal argument by providing the extensions of R(x,y) and P(x), R(x), and Q(x) in a way that makes all the formulas to the left of true and the formula on the right of false at a. Ignore the a=a: that is always true anyway.
NOTE: All of the objects must be natural numbers, i.e., 0,1,2,3 . . . The extension of a unary predicate is just a list of numbers, e.g., 1,2,4 . . .
The extension of a name is just a number, e.g., 1.
To enter the extensions of relations enter them like: , That would mean the extension of, say, R(x,y), contains those two pairs.
Remember, try to keep your domains small.
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


