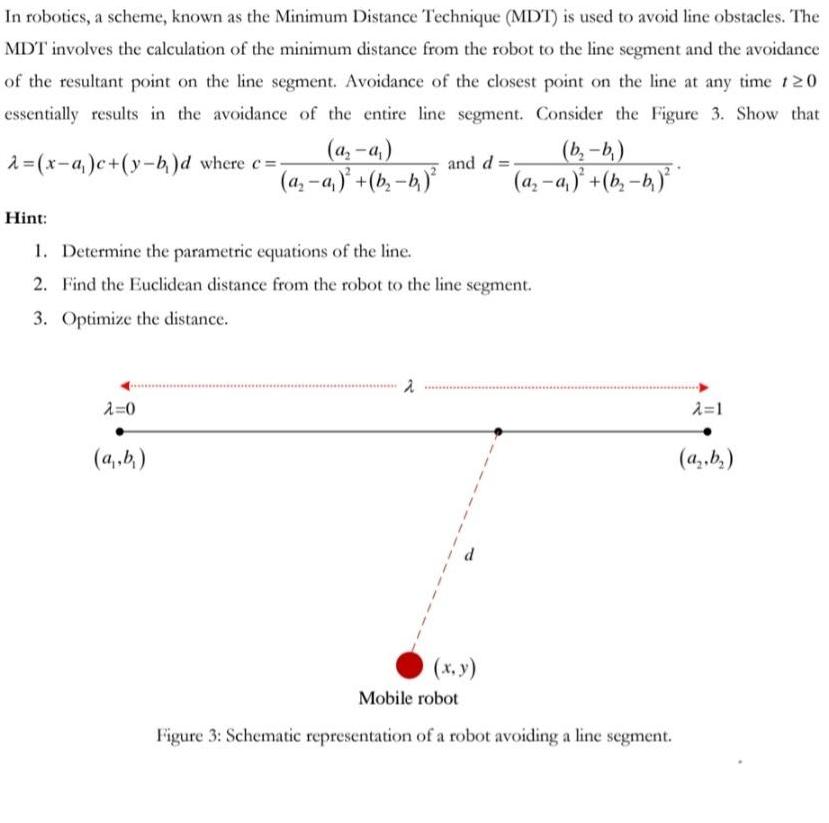
In robotics, a scheme, known as the Minimum Distance Technique (MDT) is used to avoid line obstacles. The MDT involves the calculation of the minimum distance from the robot to the line segment and the avoidance of the resultant point on the line segment. Avoidance of the closest point on the line at any time 120 essentially results in the avoidance of the entire line segment. Consider the Figure 3. Show that 2=(x-a)c+(y-b)d where c= (a-a) (a-a) + (b-b) and d = (b-b) (a-a)+(b-b) Hint: 1. Determine the parametric equations of the line. 2. Find the Euclidean distance from the robot to the line segment. 3. Optimize the distance. 2 ****** 2=0 (a,b) (x, y) Mobile robot Figure 3: Schematic representation of a robot avoiding a line segment. =1 (a.b)