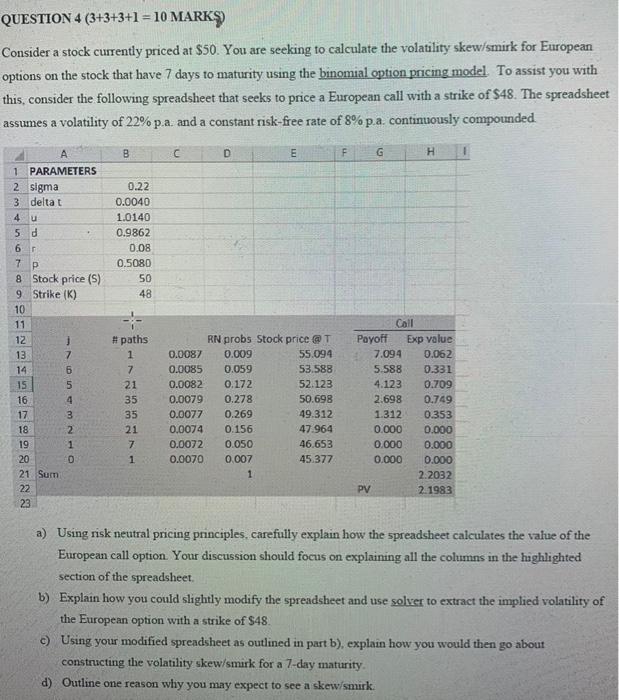
QUESTION 4 (3+3+3+1 = 10 MARK Consider a stock currently priced at $50. You are seeking to calculate the volatility skew/smirk for European options on the stock that have 7 days to maturity using the binomial option pricing model To assist you with this, consider the following spreadsheet that seeks to price a European call with a strike of $48. The spreadsheet assumes a volatility of 22% p.a. and a constant risk-free rate of 8% p.a. continuously compounded a B D E F G H 0.22 0.0040 1.0140 0.9862 0.08 0.5080 50 48 1 PARAMETERS 2 sigma 3 deltat 4 5 d 6 7 8 Stock price (5) 9 Strike (K) 10 11 12 13 7 14 6 15 5 16 4 17 3 18 2 19 1 20 21 Sum 22 23 OHNWU #paths 1 7 21 35 35 21 hasa71 RN probs Stock price @T 0.0087 0.009 55.094 0.0085 0.059 53.588 0.0082 0.172 52.123 0.0079 0.278 50.698 0.0077 0.269 49.312 0.0074 0.156 47.964 0.0072 0.050 46.653 0.0070 0.007 45.377 1 Call Payoff Exp value 7.094 0.062 5.588 0.331 4.123 0.709 2.698 0.749 1.312 0.353 0.000 0.000 0.000 0.000 0.000 0.000 2.2032 PV 2.1983 a) Using nisk neutral pricing principles, carefully explain how the spreadsheet calculates the value of the European call option. Your discussion should focus on explaining all the columns in the highlighted section of the spreadsheet. b) Explain how you could slightly modify the spreadsheet and use solver to extract the implied volatility of the European option with a strike of $48. c) Using your modified spreadsheet as outlined in part b), explain how you would then go about constructing the volatility skew/smark for a 7-day maturity d) Outline one reason why you may expect to see a skew/smik QUESTION 4 (3+3+3+1 = 10 MARK Consider a stock currently priced at $50. You are seeking to calculate the volatility skew/smirk for European options on the stock that have 7 days to maturity using the binomial option pricing model To assist you with this, consider the following spreadsheet that seeks to price a European call with a strike of $48. The spreadsheet assumes a volatility of 22% p.a. and a constant risk-free rate of 8% p.a. continuously compounded a B D E F G H 0.22 0.0040 1.0140 0.9862 0.08 0.5080 50 48 1 PARAMETERS 2 sigma 3 deltat 4 5 d 6 7 8 Stock price (5) 9 Strike (K) 10 11 12 13 7 14 6 15 5 16 4 17 3 18 2 19 1 20 21 Sum 22 23 OHNWU #paths 1 7 21 35 35 21 hasa71 RN probs Stock price @T 0.0087 0.009 55.094 0.0085 0.059 53.588 0.0082 0.172 52.123 0.0079 0.278 50.698 0.0077 0.269 49.312 0.0074 0.156 47.964 0.0072 0.050 46.653 0.0070 0.007 45.377 1 Call Payoff Exp value 7.094 0.062 5.588 0.331 4.123 0.709 2.698 0.749 1.312 0.353 0.000 0.000 0.000 0.000 0.000 0.000 2.2032 PV 2.1983 a) Using nisk neutral pricing principles, carefully explain how the spreadsheet calculates the value of the European call option. Your discussion should focus on explaining all the columns in the highlighted section of the spreadsheet. b) Explain how you could slightly modify the spreadsheet and use solver to extract the implied volatility of the European option with a strike of $48. c) Using your modified spreadsheet as outlined in part b), explain how you would then go about constructing the volatility skew/smark for a 7-day maturity d) Outline one reason why you may expect to see a skew/smik