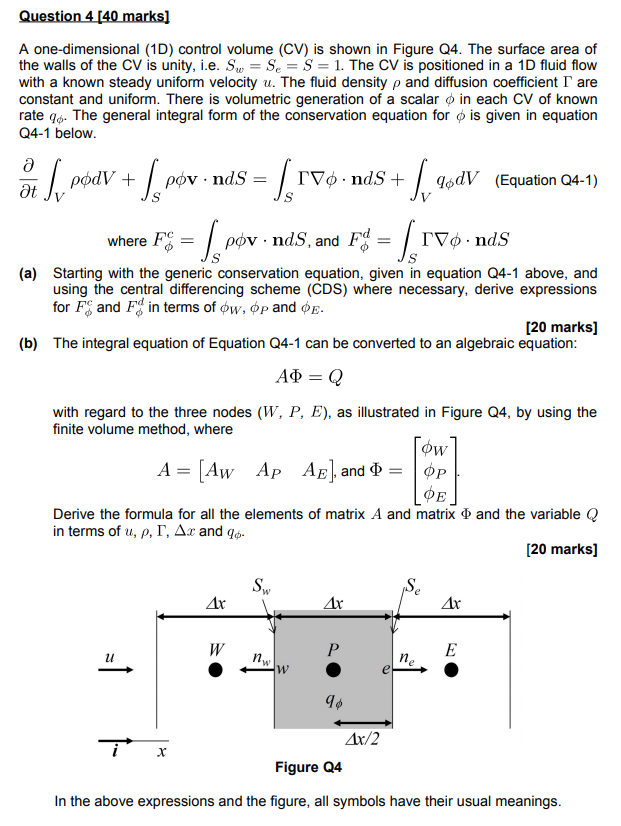
Question 4 [40 marks] A one-dimensional (1D) control volume (CV) is shown in Figure Q4. The surface area of the walls of the CV is unity, i.e. S = Se = S = 1. The CV is positioned in a 1D fluid flow with a known steady uniform velocity u. The fluid density p and diffusion coefficient I are constant and uniform. There is volumetric generation of a scalar in each CV of known rate q4. The general integral form of the conservation equation for is given in equation Q4-1 below. t v podV+ [pov pov nds = rVonds + 96dV (Equation Q4-1) where F =pov nds, and Fd = TVO.ndS = S (a) Starting with the generic conservation equation, given in equation Q4-1 above, and using the central differencing scheme (CDS) where necessary, derive expressions for F and F in terms of ow, op and OE. [20 marks] (b) The integral equation of Equation Q4-1 can be converted to an algebraic equation: = Q with regard to the three nodes (W, P, E), as illustrated in Figure Q4, by using the finite volume method, where A= [Aw Ap AE], and > = ow Derive the formula for all the elements of matrix A and matrix and the variable Q in terms of u, p, r, Ax and q [20 marks] Sw Ax Ax Ax W P E nw W ne e ix 9$ Figure Q4 Ax/2 In the above expressions and the figure, all symbols have their usual meanings.