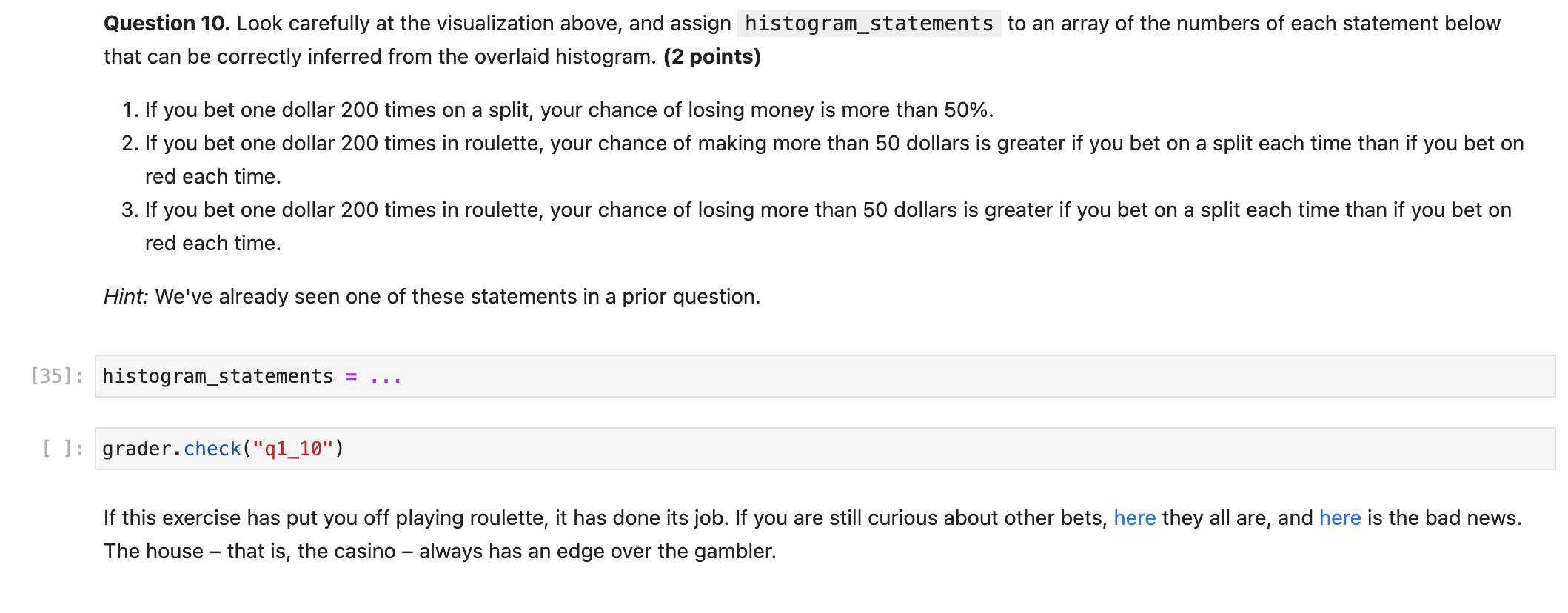
Question 5. Complete the cell below to simulate the net gain in 200 one-dollar bets on red, repeating the process 10,000 times. After the cell is run, simulated_gains_red should be an array with 10,000 entries, each of which is the net gain in 200 one-dollar bets on red. (4 points) Hint: Think about which computational tool might be helpful for simulating a process multiple times. Lab 5 might be a good resource to look at! Note: This cell might take a few seconds to run. num_bets =10000 repetitions = simulated_gains_red = len(simulated_gains_red) \# Do not change this line! Check that simulated_gains_red is length 10000. grader.check("q1_5") Run the cell below to visualize the results of your simulation. Question 6: Using the histogram above, decide whether the following statement is true or false: If you make 200 one-dollar bets on red, your chance of losing money is more than 50%. Assign to either or depending on your answer to the question. (2 points) \[ \text { loss_more_than_50 }=\ldots \] grader. check("q1_6") Betting on a Split If betting on red doesn't seem like a good idea, maybe a gambler might want to try a different bet. A bet on a split is a bet on two consecutive numbers such as 5 and 6 . This bets pays 17 to 1 . That means if you place a one-dollar bet on the split 5 and 6 , then: - If the winning pocket is either 5 or 6 , your gain is 17 dollars. - If any other pocket wins, you lose your dollar, so your gain is 1 dollars. Question 7. Define a function dollar_bet_on_split that takes a pocket number and returns your gain in dollars if that pocket won and you had bet one dollar on the 56 split. ( 4 points) Hint: Remember that the pockets are represented as strings. \[ \begin{array}{l} \text { def dollar_bet_on_split }(. . .) \text { : } \\ \ldots \\ \text { grader. check("q1_7") } \end{array} \] Run the cell below to check that your function is doing what it should. print(dollar_bet_on_split('23')) Question 8. Add a column Winnings: Split to the wheel table. For each pocket, the column should contain your gain in dollars if that pocket won and you had bet one dollar on the 56 split. (4 points) split_winnings = wheel = wheel.show(5) \# Do not change this line. grader.check("q1_8") Question 9. Simulate the net gain in 200 one-dollar bets on the 5-6 split, repeating the process 10,000 times and saving your gains in the array simulated_gains_split.(5 points) Hint: Your code in Questions 4 and 5 may be helpful here! 2] : simulated_gains_split = \# Do not change the two lines below gains = gains.with_columns('Net Gain on Split', simulated_gains_split) gains.hist(bins = np.arange (200,150,20)) Question 10. Look carefully at the visualization above, and assign histogram_statements to an array of the numbers of each statement below that can be correctly inferred from the overlaid histogram. (2 points) 1. If you bet one dollar 200 times on a split, your chance of losing money is more than 50%. 2. If you bet one dollar 200 times in roulette, your chance of making more than 50 dollars is greater if you bet on a split each time than if you bet on red each time. 3. If you bet one dollar 200 times in roulette, your chance of losing more than 50 dollars is greater if you bet on a split each time than if you bet on red each time. Hint: We've already seen one of these statements in a prior question. histogram_statements = grader.check("q1_10") If this exercise has put you off playing roulette, it has done its job. If you are still curious about other bets, here they all are, and here is the bad news. The house - that is, the casino - always has an edge over the gambler