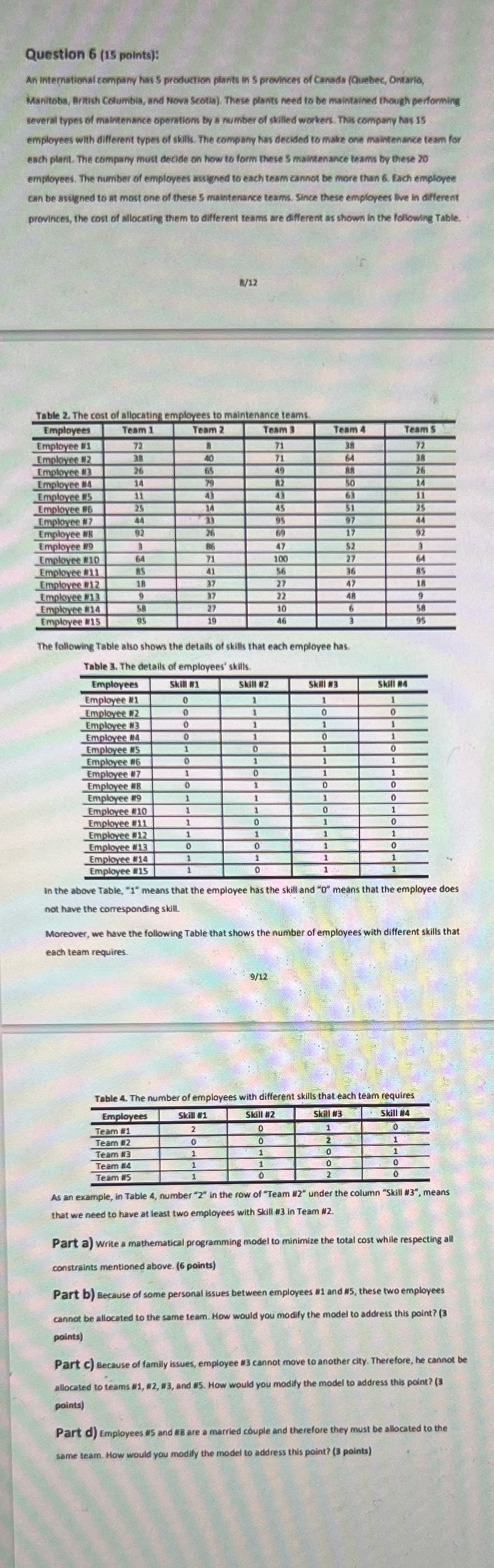
Question 6 (15 points): An international company has S production plants in S provinces of Canada (Quebec, Ontario, Manitoba, British Columbia, and Nova Scotia). These plants need to be maintained though performing several types of maintenance operations by a number of skilled workers. This company has 15 employees with different types of skills. The company has decided to make one maintenance team for each plant. The company must decide on how to form these 5 maintenance teams by these 20 employees. The number of employees assigned to each team cannot be more than 6. Each employee can be assigned to at most one of these S maintenance teams. Since these employees live in different provinces, the cost of allocating them to different teams are different as shown in the following Table, 8/12 Employees Team 1 Employee #1 72 Employee #2 Employee #3 Employee Na Employee #S Employee #6 25 Employee Ny 44 Employee NB 92 Employee #9 Employee RID 64 Employee #11 Employee #12 Employee #13 Employee #14 Employee #15 Employees Skill #1 Skill #2 Skill #3 Skill 84 Employee #1 Employee #2 0 Employee #3 Employee #4 Employee NS Employees Employee *7 Employee NB Employee #9 Employee #10 Employee #11 Employee #12 Employee #13 Employee #14 Employee #15 In the above Table, "1" means that the employee has the skill and "D" means that the employee does not have the corresponding skill. Moreover, we have the following Table that shows the number of employees with different skills that each team requires. Table 4. The number of employees with different skills that each team requires Employees Skill #1 Skill #12 Skill #3 Skill #4 Team #1 Team #2 0 Team HE Team #4 Team #5 As an example, in Table 4, number "2" in the row of "Team 12" under the column "Skill #3", means that we need to have at least two employees with Skill #3 in Team #z. Part a) Write a mathematical programming model to minimize the total cost while respecting all constraints mentioned above. (6 points) Part b) Because of some personal issues between employees ill and #5, these two employees cannot be allocated to the same team. How would you modify the model to address this point? (3 points) Part c) Because of family issues, employee #3 cannot move to another city. Therefore, he cannot be allocated to teams #1, #2, #3, and #5. How would you modify the model to address this point? (3 points) Part d) Employees #5 and #18 are a married couple and therefore they must be allocated to the same team. How would you modify the model to address this point? (3 points)