Question:
Buses arrive at a bus station with i.i.d. interarrival times following an exponential distribution with intensity ?. Alice arrives at the bus station at a deterministic time t. a. (4pts) What is the expected waiting time for Alice until next bus comes? b. (6pts) Let ? be the time when the last bus arrived before time t. Show that t ? ? follows an exponential distribution with parameter ?. c. (6pts) Show that the expected interarrival time between the last bus which arrived before time t and the first bus which arrives after time t is 2 ? . Explain why it is different from the general expected interarrival time 1 ? .
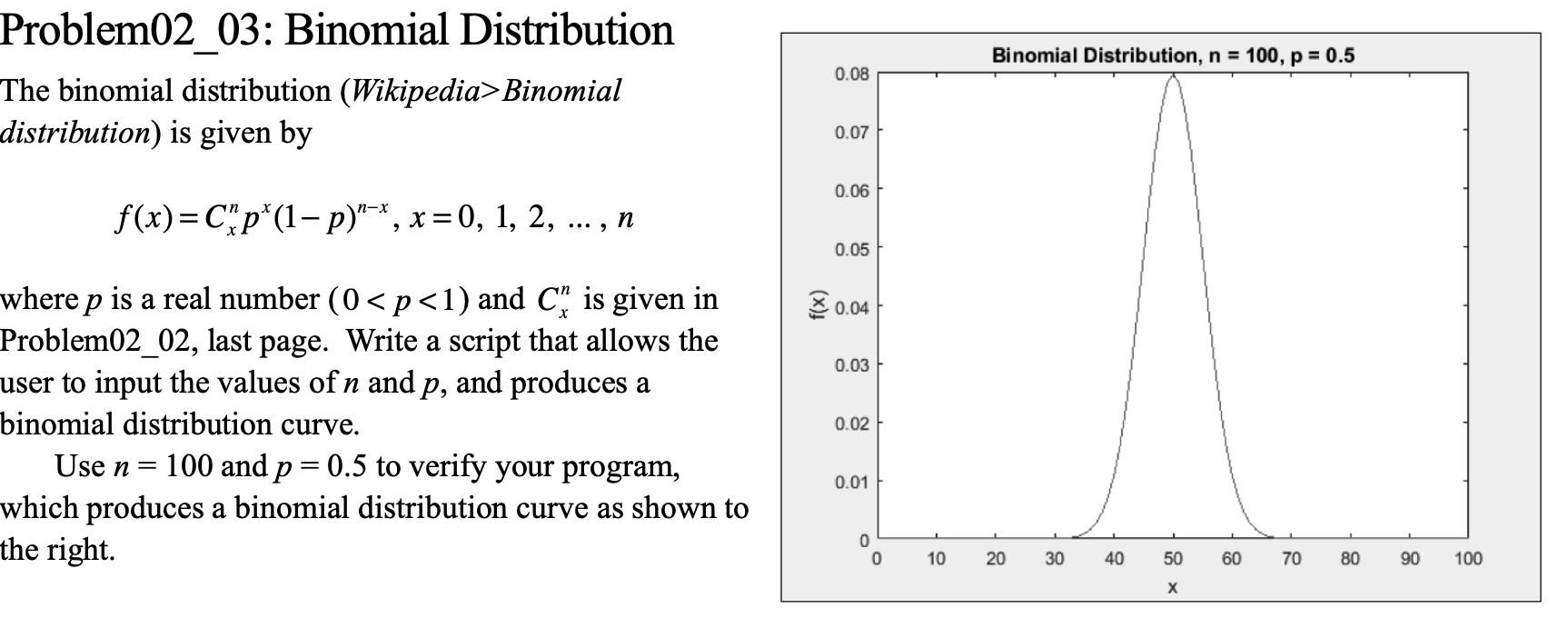
In each situation below, is it reasonable to use a binomial distribution for the random variable X? Give reasons for your answerin each case. {a} A random sample of students in a fitness study. X is the mean systolic blood pressure of the sample. tries, a binomial distnbution is reasonable. X can only take on two values No, a binomial distnbution is not reasonable. X is not a count of successes. No; a binomial tstribution is not reasonable. Binomial distnbutions cannot be used with random samples No, a binomial tstribution is not reasonable. it should be associated with a population \"ms a binomial tstribution is reasonable. X is a mean of the binomial distribution. [bi A manufacturer of running shoes picks a random sample o'fthe production of shoes each day for a detailed inspection. Today's sample of 20 pairs of shoes indudes 1 pairwith a defect. No; a binomial bstribution is not reasonable. Dne defect in a sample of 2B is not a large enough percentage. No, a binomial distribution is not reasonable. Binomial distributions cannot be used with random samples. \"ms a binomial distribution is reasonable. p is the probability of a defective pair. "ms a binomial distribution is reasonable. p is the number of defective shoes from today's sample. No, a binomial distribution is not reasonable. Cine defect is not a large enough count. {c} A nutrition study d'iooses an SR5 of college students Tl'iey are asked whether or not they usually eat at least ve servings of fruits or vegetables per day. X is the nurrberwho saythat they do. \"lies; a binomial distribution is reasonable. n is the number of students chosen from the sample and X is the number of servings of fmits and vegetables they eat. No, a binomial tstribuijon is not reasonable. A student might eat less than ve senaings offnJits and vegetables but could daim othenlvise. Yes, a binomial distnbution is reasonable. p is the percentage of students d'iosen from the population and n is the number of servings of fmits. and vegetables they eat. Yes, a binomial distnbution is reasonable. n is the number of students in the sample and p is the probabilitythat a student eats at least five servings o'ffruits and vegetables No, a binomial tstribution is not reasonable. Binomial distnbutions cannot be used with random samples Problem02_03: Binomial Distribution The binomial distribution (Wiklpedia>Bin0mial distribution) is given by f(x)=C:p"(1p)"'x, x =0, 1, 2, , n where p is a real number (0