Question Content Area

Problem 14-01 (Algorithmic)

The RMC Corporation blends three raw materials to produce two products: a fuel additive and a solvent base. Each ton of fuel additive is a mixture of 1/2 ton of material 1 and 1/2 ton of material 3. A ton of solvent base is a mixture of 1/5 ton of material 1, 3/5 ton of material 2, and 1/5 ton of material 3. RMCs production is constrained by a limited availability of the three raw materials. For the current production period, RMC has the following quantities of each raw material: material 1, 16 tons; material 2, 18 tons; material 3, 12 tons. Management wants to achieve the following P₁ priority level goals:

Goal 1: Produce at least 20 tons of fuel additive.

Goal 2: Produce at least 15 tons of solvent base.

Assume there are no other goals.

1. Is it possible for management to achieve both P₁ level goals given the constraints on the amounts of each material available?

   	Amount needed to
   Raw Material	Achieve Both P1 Goals
   1	fill in the blank 1
   2	fill in the blank 2
   3	fill in the blank 3

2. Treating the amounts of each material available as constraints, formulate a goal programming model to determine the optimal product mix. Assume that both P₁ priority level goals are equally important to management. If you don't need the variable in the model, enter "0". If you need a negative number, enter minus sign with it. If necessary, enter the numbers as a common fraction.

   Let
   	x1 = the number of tons of fuel additive produced
   	x2 = the number of tons of solvent base produced
   	d1+ = the amount by which the number of tons of fuel additive produced exceeds the target value of 20 tons
   	d1- = the amount by which the number of tons of fuel additive produced is less than the target of 20 tons
   	d2+ = the amount by which the number of tons of solvent base produced exceeds the target value of 15 tons
   	d2- = the amount by which the number of tons of solvent base is less than the target value of 15 tons

   Min	fill in the blank 5d1-	+	fill in the blank 6d2-
   s.t.
   	x1	+	x2						fill in the blank 9	Material 1
   	fill in the blank 10x1	+	x2						fill in the blank 12	Material 2
   	x1	+	x2						fill in the blank 15	Material 3
   	fill in the blank 16x1	+	fill in the blank 17x2	+	fill in the blank 18d1+	+	fill in the blank 19d1-	=	fill in the blank 20	Goal 1
   	fill in the blank 21x1	+	fill in the blank 22x2	+	fill in the blank 23d2+	+	fill in the blank 24d2-	=	fill in the blank 25	Goal 2
   x1, x2, d1+, d1-, d2+, d2- 0

3. Choose the correct graph that solves the model formulated in part b.

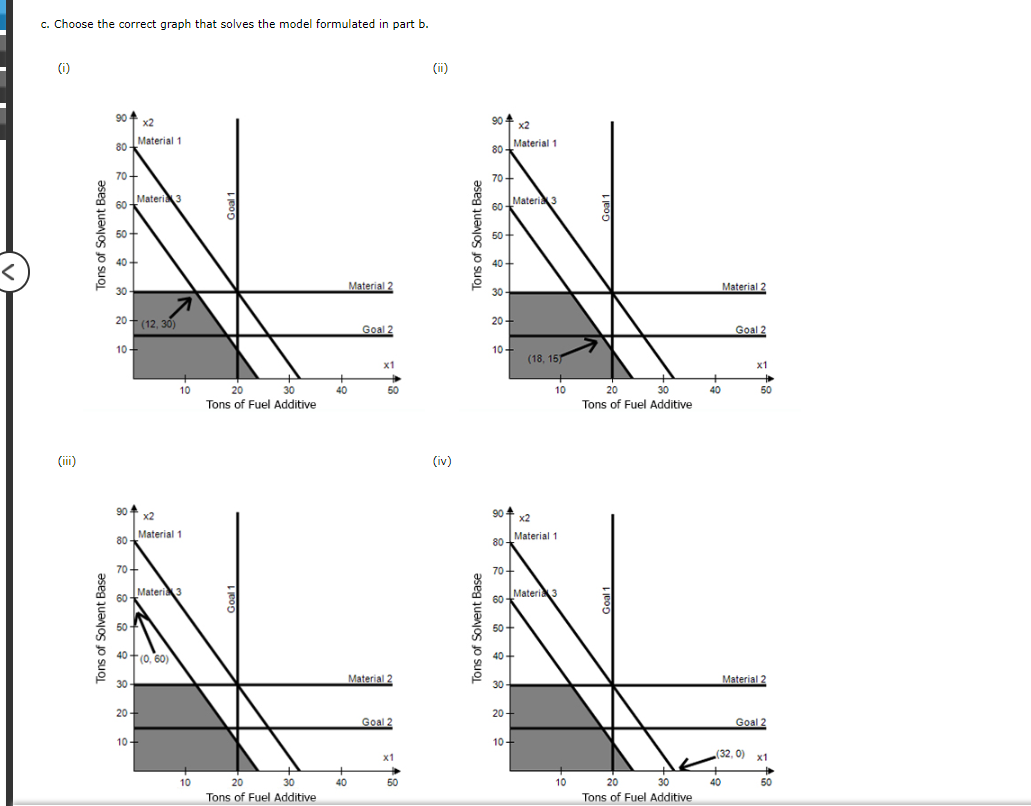
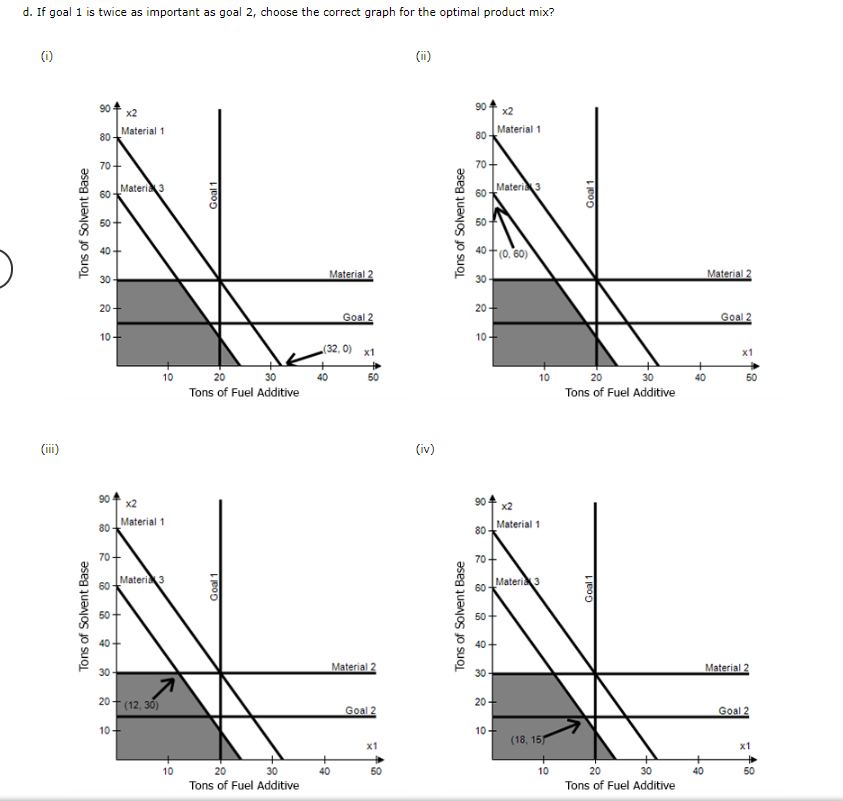
Problem 14-01 (Algorithmic) The RMC Corporation blends three raw materials to produce two products: a fuel additive and a solvent base. Each ton of fuel additive is a mixture of 1/2 ton of material 1 and 1/2 ton of material 3. A ton of solvent base is a mixture of 1/5 ton of material 1, 3/5 ton of material 2, and 1/5 ton of material 3. RMC's production is constrained by a limited availability of the three raw materials. For the current production period, RMC has the following quantities of each raw material: material 1, 16 tons; material 2, 18 tons; material 3, 12 tons. Management wants to achieve the following P1 priority level goals: Goal 1: Produce at least 20 tons of fuel additive. Goal 2: Produce at least 15 tons of solvent base. Assume there are no other goals. a. Is it possible for management to achieve both P1 level goals given the constraints on the amounts of each material available? Raw Material 1 2 3 Amount needed to Achieve Both P1 Goals b. Treating the amounts of each material available as constraints, formulate a goal programming model to determine the optimal product mix. Assume that both P1 priority level goals are equally important to management. If you don't need the variable in the model, enter "0". If you need a negative number, enter minus sign with it. If necessary, enter the numbers as a common fraction. Let x1 = the number of tons of fuel additive produced x2 = the number of tons of solvent base produced di+ = the amount by which the number of tons of fuel additive produced exceeds the target value of 20 tons d = the amount by which the number of tons of fuel additive produced is less than the target of 20 tons d2+ = the amount by which the number of tons of solvent base produced exceeds the target value of 15 tons d2 = the amount by which the number of tons of solvent base is less than the target value of 15 tons Min s.t. x1 x1 d1 X1 X1 X1 + + + + + + X2 x2 x2 d2 x2 x2 + + d+ + d2+ + x1, x2, d1+, di, d+, d2 0 d1 d2 S VI VI = = Material 1 Material 2 Material 3 Goal 1 Goal 2 c. Choose the correct graph that solves the model formulated in part b. (1) 20 9 Tons of Solvent Base 8 8 9 8 o 8 o Tons of Solvent Base 8 8 9 Goal 1 10 20 30 Tons of Fuel Additive Goal 1 10 20 30 Tons of Fuel Additive 40 9 Material 2 Goal 2 8 (iv) 89 2 8 Tons of Solvent Base 8 8 8 8 2 g Tons of Solvent Base 8 8 8 20 S Material 1 Goal 1 20 30 Tons of Fuel Additive Goal 1 20 30 Tons of Fuel Additive 9 Material 2 Goal 2 8, Material 2 (32,0) +8 d. If goal 1 is twice as important as goal 2, choose the correct graph for the optimal product mix? (1) (iii) Tons of Solvent Base Tons of Solvent Base 90 80 70+ 60 50 9 30 20+ x2 Material 1 10+ 80 90 x2 Materia 3 60 50 70+ 30 Material 1 10 Materi 3 20 (12,30) 10+ 10 Goal 1 20 30 Tons of Fuel Additive Goal 1 20 30 Tons of Fuel Additive Material 2 40 (32,0) x1 Goal 2 40 50 Material 2 Goal 2 x1 50 (ii) (iv) Tons of Solvent Base Tons of Solvent Base 90 80 70 60 50 30 40 (0, 60) 20+ 90 10+ 80 70 60 50 Materia 3 9 x2 Material 1 30 x2 Material 1 20+ 10 Materi 3 10+ (18, 15 10 Goal 1 20 30 Tons of Fuel Additive Goal 1 20 30 Tons of Fuel Additive 40 Material 2 Goal 2 x1 60 Material 2 Goal 2 x1 + 50 Problem 14-01 (Algorithmic) The RMC Corporation blends three raw materials to produce two products: a fuel additive and a solvent base. Each ton of fuel additive is a mixture of 1/2 ton of material 1 and 1/2 ton of material 3. A ton of solvent base is a mixture of 1/5 ton of material 1, 3/5 ton of material 2, and 1/5 ton of material 3. RMC's production is constrained by a limited availability of the three raw materials. For the current production period, RMC has the following quantities of each raw material: material 1, 16 tons; material 2, 18 tons; material 3, 12 tons. Management wants to achieve the following P1 priority level goals: Goal 1: Produce at least 20 tons of fuel additive. Goal 2: Produce at least 15 tons of solvent base. Assume there are no other goals. a. Is it possible for management to achieve both P1 level goals given the constraints on the amounts of each material available? Raw Material 1 2 3 Amount needed to Achieve Both P1 Goals b. Treating the amounts of each material available as constraints, formulate a goal programming model to determine the optimal product mix. Assume that both P1 priority level goals are equally important to management. If you don't need the variable in the model, enter "0". If you need a negative number, enter minus sign with it. If necessary, enter the numbers as a common fraction. Let x1 = the number of tons of fuel additive produced x2 = the number of tons of solvent base produced di+ = the amount by which the number of tons of fuel additive produced exceeds the target value of 20 tons d = the amount by which the number of tons of fuel additive produced is less than the target of 20 tons d2+ = the amount by which the number of tons of solvent base produced exceeds the target value of 15 tons d2 = the amount by which the number of tons of solvent base is less than the target value of 15 tons Min s.t. x1 x1 d1 X1 X1 X1 + + + + + + X2 x2 x2 d2 x2 x2 + + d+ + d2+ + x1, x2, d1+, di, d+, d2 0 d1 d2 S VI VI = = Material 1 Material 2 Material 3 Goal 1 Goal 2 c. Choose the correct graph that solves the model formulated in part b. (1) 20 9 Tons of Solvent Base 8 8 9 8 o 8 o Tons of Solvent Base 8 8 9 Goal 1 10 20 30 Tons of Fuel Additive Goal 1 10 20 30 Tons of Fuel Additive 40 9 Material 2 Goal 2 8 (iv) 89 2 8 Tons of Solvent Base 8 8 8 8 2 g Tons of Solvent Base 8 8 8 20 S Material 1 Goal 1 20 30 Tons of Fuel Additive Goal 1 20 30 Tons of Fuel Additive 9 Material 2 Goal 2 8, Material 2 (32,0) +8 d. If goal 1 is twice as important as goal 2, choose the correct graph for the optimal product mix? (1) (iii) Tons of Solvent Base Tons of Solvent Base 90 80 70+ 60 50 9 30 20+ x2 Material 1 10+ 80 90 x2 Materia 3 60 50 70+ 30 Material 1 10 Materi 3 20 (12,30) 10+ 10 Goal 1 20 30 Tons of Fuel Additive Goal 1 20 30 Tons of Fuel Additive Material 2 40 (32,0) x1 Goal 2 40 50 Material 2 Goal 2 x1 50 (ii) (iv) Tons of Solvent Base Tons of Solvent Base 90 80 70 60 50 30 40 (0, 60) 20+ 90 10+ 80 70 60 50 Materia 3 9 x2 Material 1 30 x2 Material 1 20+ 10 Materi 3 10+ (18, 15 10 Goal 1 20 30 Tons of Fuel Additive Goal 1 20 30 Tons of Fuel Additive 40 Material 2 Goal 2 x1 60 Material 2 Goal 2 x1 + 50