Question:
Hello! I do not understand what the following question asks for a. subquestion. I feel confused. Can someone provide me with a detailed explanation? Thank you!
1. Go to the All Locations worksheet, where Benicio wants to summarize the quarterly and annual totals from the three locations for each type of product.
Consolidate the sales data from the three locations as follows:
a. In cell B5, enter a formula using the SUM function and 3-D references that totals the Mini sales values (cell B5) in Quarter 1 from the U.S., Canada, and Mexico worksheets.
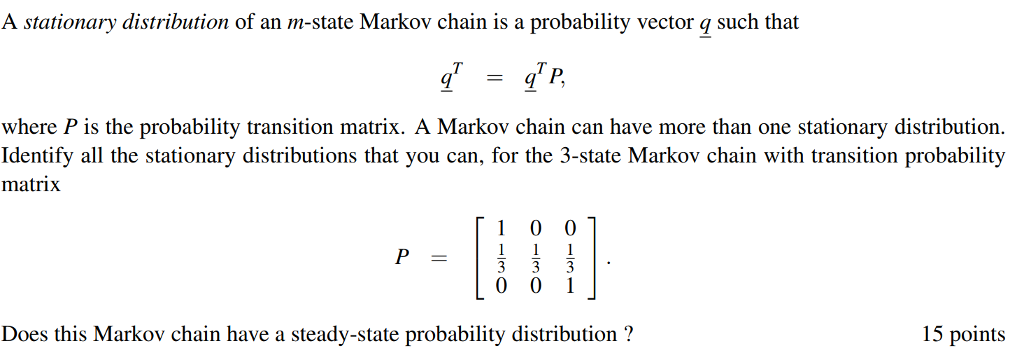
2. (10 points) Consider a continuous-time Markov chain with the transition rate matrix 4 2 2 Q = 3 1 CT 0 (a) What is the expected amount of time spent in each state? (b) What is the transition probability matrix of the embedded discrete-time Markov chain? (c) Is this continuous-time Markov chain irreducible? (d) Compute the stationary distribution for the continuous-time Markov chain and the em- bedded discrete-time Markov chain and compare the two.A Markov chain with state space {1, 2, 3} has transition probability matrix 0.6 0.3 0.1\\ P. = 0.3 0.3 0.4 0.4 0.1 0.5 (a) Is this Markov chain irreducible? Is the Markov chain recurrent or transient? Explain your answers. (b) What is the period of state 1? Hence deduce the period of the remaining states. Does this Markov chain have a limiting distribution? (c) Consider a general three-state Markov chain with transition matrix P11 P12 P13 P = P21 P22 P23 P31 P32 P33 Give an example of a specific set of probabilities p;; for which the Markov chain is not irreducible (there is no single right answer to this, of course !).A stationary distribution of an m-state Markov chain is a probability vector q such that = q P, where P is the probability transition matrix. A Markov chain can have more than one stationary distribution. Identify all the stationary distributions that you can, for the 3-state Markov chain with transition probability matrix O O P Owl Does this Markov chain have a steady-state probability distribution ? 15 pointsConsider a standard chessboard with an 8 x 8 grid of possible locations. We define a Markov chain by randomly moving a single chess piece on this board. The initial location Xo is sampled uniformly among the 82 = 64 squares. At time t, the piece then chooses Xt+1 by sampling uniformly from the set of legal moves given its current location Xt. For a description of legal chess moves, see: http://en. wikipedia. org/wiki/Rules_of_chess#Basic_moves. a) Suppose the chess piece is a king, which can move to any of the 8 adjacent squares. Is the Markov chain irreducible? Is the Markov chain aperiodic? b) Suppose the chess piece is a bishop. Is the Markov chain irreducible? Is the Markov chain aperiodic? c) Suppose the chess piece is a knight. Is the Markov chain irreducible? Is the Markov chain aperiodic