Question M the answer is incorrect so can someone please help me
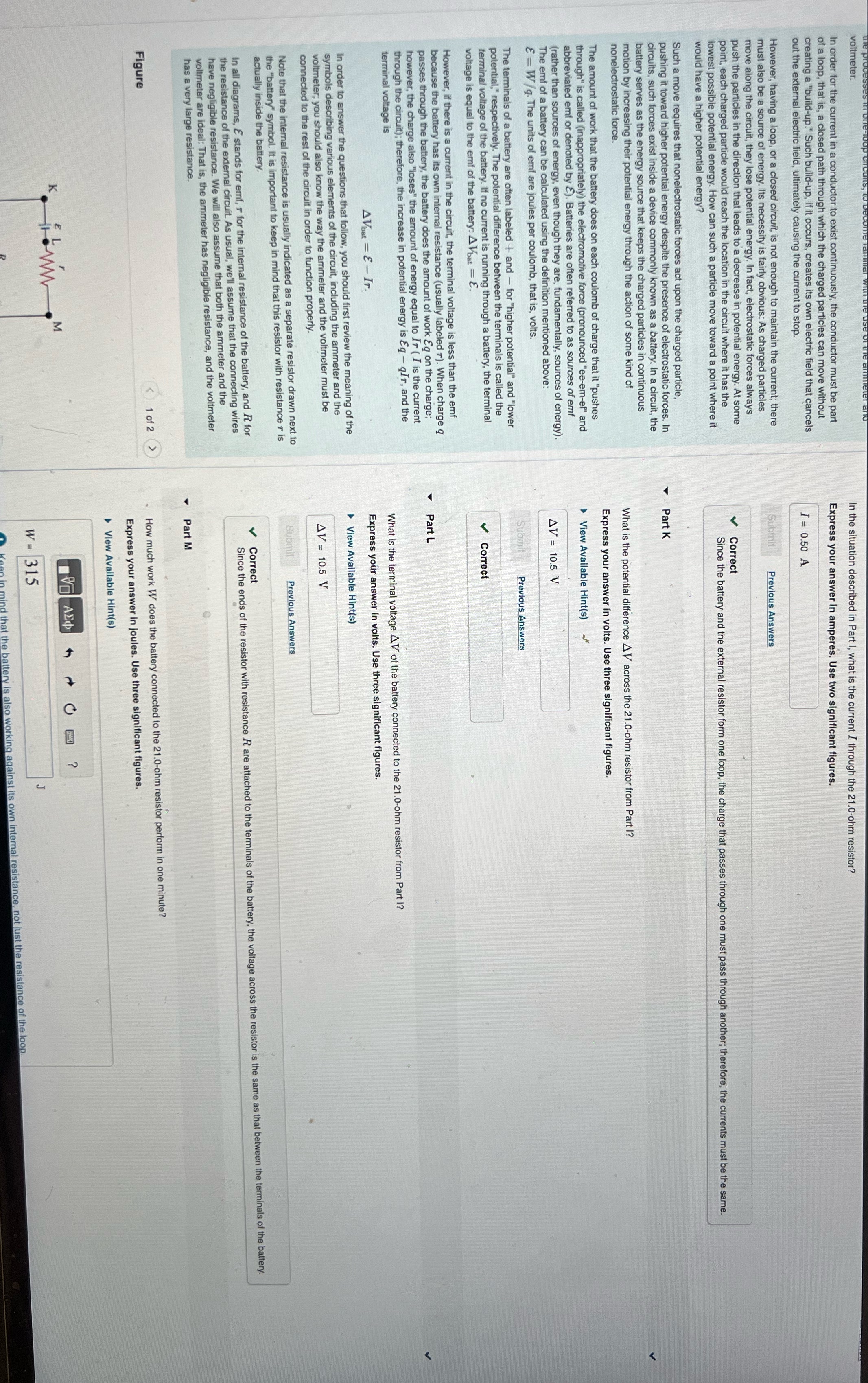
voltmeter. In the situation described in Part I, what is the current I through the 21.0-ohm resistor? In order for the current in a conductor to exist continuously, the conductor must be part of a loop, that is, a closed path through which the charged particles can move without Express your answer in amperes. Use two significant figures. creating a "build-up." Such build-up, if it occurs, creates its own electric field that cancels out the external electric field, ultimately causing the current to stop. I = 0.50 A However, having a loop, or a closed circuit, is not enough to maintain the current; there must also be a source of energy. Its necessity is fairly obvious: As charged particles Submit Previous Answers move along the circuit, they lose potential energy. In fact, electrostatic forces always push the particles in the direction that leads to a decre decrease in potential energy. At some point, each charged particle would reach the location in the circuit where it has the Correct lowest possible potential energy. How can such a particle move toward a point where it Since the battery and the external resistor form one loop, the charge that passes through one must pass through another; therefore, the currents must be the same. would have a higher potential energy? Such a move requires that nonelectrostatic forces act upon the charged particle, pushing it toward higher potential energy despite the presence of electrostatic forces. In Part K circuits, such forces exist inside a device commonly known as a battery. In a circuit, the battery serves as the energy source that keeps the charged particles in continuous motion by increasing their potential energy through the action of some kind of nonelectrostatic force. What is the potential difference A V across the 21.0-ohm resistor from Part I? The amount of work that the battery does on each coulomb of charge that it "pushes Express your answer in volts. Use three significant figures. through" is called (inappropriately) the electromotive force (pronounced "ee-em-ef" and View Available Hint(s) abbreviated emf or denoted by &). Batteries are often referred to as sources of emf (rather than sources of energy, even though they are, fundamentally, sources of energy). The emi of a battery can be calculated using the definition mentioned above: AV = 10.5 V E = W/ q. The units of emf are joules per coulomb, that is, volts. Submit Previous Answers The terminals of a battery are often labeled + and - for "higher potential" and "lower potential," respectively. The potential difference between the terminals is called the terminal voltage of the battery. If no current is running through a battery, the terminal Correct voltage is equal to the emf of the battery: A Vbat = However, if there is a current in the circuit, the terminal voltage is less than the emf because the battery has its own internal resistance (usually labeled r). When charge q passes through the battery, the battery does the amount of work &g on the charge; Part L however, the charge also "loses" the amount of energy equal to Ir ( I is the current through the circuit); therefore, the increase in potential energy is Eq - qIr, and the terminal voltage is What is the terminal voltage AV of the battery connected to the 21.0-ohm resistor from Part I? AVbat = E - IT. Express your answer in volts. Use three significant figures. In order to answer the questions that follow, you should first review the meaning of the View Available Hint(s) symbols describing various elements of the circuit, including the ammeter and the voltmeter; you should also know the way the ammeter and the voltmeter must be AV = 10.5 V connected to the rest of the circuit in order to function properly. Note that the internal resistance is usually indicated as a separate resistor drawn next to Submit Previous Answers the "battery" symbol. It is important to keep in mind that this resistor with resistance r is actually inside the battery. Correct In all diagrams, & stands for emf, r for the internal resistance of the battery, and R for Since the ends of the resistor with resistance R are attached to the terminals of the battery, the voltage across the resistor is the same as that between the terminals of the battery. the resistance of the external circuit. As usual, we'll assume that the connecting wires have negligible resistance. We will also assume that both the ammeter and the voltmeter are ideal: That is, the ammeter has negligible resistance, and the voltmeter has a very large resistance. Part M Figure How much work W does the battery connected to the 21.0-ohm resistor perform in one minute ? Express your answer in Joules. Use three significant figures. > View Available Hint(s) M AEd W = 315 is also working against its own internal resistance, not just the resistance of the loop