Question:

Prove 6.46 and 6.47

Reference:

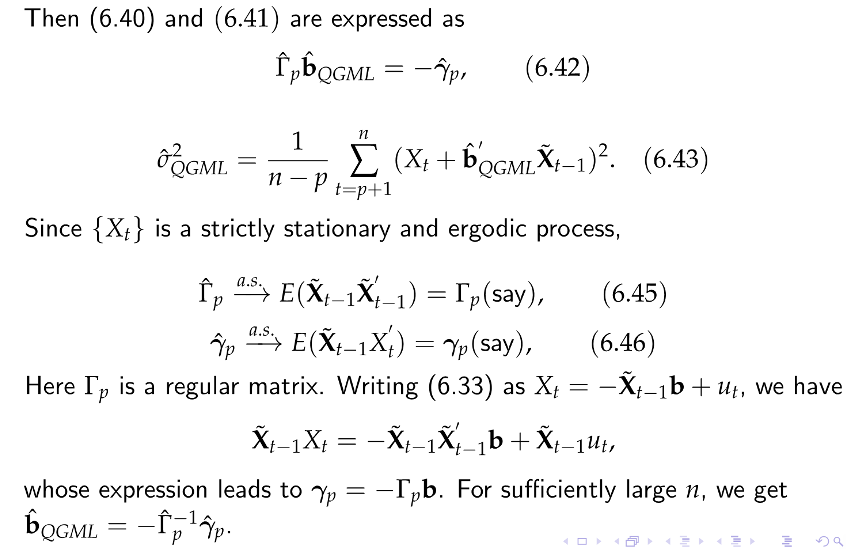
= = Let b = (b1, . . . , bp) and t1 = (X41,...,Xt-p)'. Then the solutions b = HQGML and o2 = @@GML of the equations = 21 (0) 1 n1 [ /t-1(X+ + bX41 + + bpX4-p) = 0, (6.40) = ab 02 t=p+1 ali (e) 11 (X: +b X,-1+...+bqXt-p)2 = 0(6.41) = ( = n-p 1 1 2 + 2 o2 204 t=p+1 become their QGMLE. Write 11 1 X-1Xt-1 P n - P t=p+1 (- - - X = n 1 @up = X-1. n-P t=p+1 X-X a na Then (6.40) and (6.41) are expressed as QGML --Wp, (6.42) 11 1 . = (X: + BOGMt1)2 (6.43) QGML n-p t=p+1 Since {Xt} is a strictly stationary and ergodic process, = a.s. = = - , a.s., E(X:-1X, -1) = [p(say), (6.45) p 4.5, E(X+-1X/) = yp(say), (6.46) Here Ip is a regular matrix. Writing (6.33) as X+ = -X-1b + ut, we have XI-1X+ = - X:-1X41b + X:-107, whose expression leads to Yp = -1pb. For sufficiently large n, we get bQGML -rlp = - = From (6.44) and (6.45) it follows that a.s. bogml 4.S, b. b (6.46) On the other hand, 11 1 = QGML [ {ut + (HQGML b) X{1}2 n-p t=p+1 11 n 1 1 = [ u +2(bGML b) - X-1 n - P n - P t=p+1 t=p+1 11 1 +(bcm. by{n=p, X-X1}(60cm b) ) xbQcm nP =p+1 (6.47) = (A) + (B) + (C), say. a na a.s. We can see that (A) 4.5., o2 and 11 11 1 a.s. 1 -0. , 0 , LuX-1 4.S., O, t=p+1 , , Xt-18:41 4.5Ip, (6.48) X X- n-p n - P - t=p+1 17.S. a.s. = 0 and (C) ">> 0. Therefore we have hence, together with (6.46), (B) @@GML 4.57 02, and o2 a.s. s vn(begml b) ] Vn (W. 02) 1-1 OGML - 1 pn-p 1 =p+1 }}-{- viena 8-14 + , = (t = +1(u? 02) } +0(1), a.s. (6.49) ) Vn-p 2t=p+1 Applying the Cramr-Wold device and Theorem 5.9 to the right-hand side of (6.49) we obtain the following theorem. a na = = Let b = (b1, . . . , bp) and t1 = (X41,...,Xt-p)'. Then the solutions b = HQGML and o2 = @@GML of the equations = 21 (0) 1 n1 [ /t-1(X+ + bX41 + + bpX4-p) = 0, (6.40) = ab 02 t=p+1 ali (e) 11 (X: +b X,-1+...+bqXt-p)2 = 0(6.41) = ( = n-p 1 1 2 + 2 o2 204 t=p+1 become their QGMLE. Write 11 1 X-1Xt-1 P n - P t=p+1 (- - - X = n 1 @up = X-1. n-P t=p+1 X-X a na Then (6.40) and (6.41) are expressed as QGML --Wp, (6.42) 11 1 . = (X: + BOGMt1)2 (6.43) QGML n-p t=p+1 Since {Xt} is a strictly stationary and ergodic process, = a.s. = = - , a.s., E(X:-1X, -1) = [p(say), (6.45) p 4.5, E(X+-1X/) = yp(say), (6.46) Here Ip is a regular matrix. Writing (6.33) as X+ = -X-1b + ut, we have XI-1X+ = - X:-1X41b + X:-107, whose expression leads to Yp = -1pb. For sufficiently large n, we get bQGML -rlp = - = From (6.44) and (6.45) it follows that a.s. bogml 4.S, b. b (6.46) On the other hand, 11 1 = QGML [ {ut + (HQGML b) X{1}2 n-p t=p+1 11 n 1 1 = [ u +2(bGML b) - X-1 n - P n - P t=p+1 t=p+1 11 1 +(bcm. by{n=p, X-X1}(60cm b) ) xbQcm nP =p+1 (6.47) = (A) + (B) + (C), say. a na a.s. We can see that (A) 4.5., o2 and 11 11 1 a.s. 1 -0. , 0 , LuX-1 4.S., O, t=p+1 , , Xt-18:41 4.5Ip, (6.48) X X- n-p n - P - t=p+1 17.S. a.s. = 0 and (C) ">> 0. Therefore we have hence, together with (6.46), (B) @@GML 4.57 02, and o2 a.s. s vn(begml b) ] Vn (W. 02) 1-1 OGML - 1 pn-p 1 =p+1 }}-{- viena 8-14 + , = (t = +1(u? 02) } +0(1), a.s. (6.49) ) Vn-p 2t=p+1 Applying the Cramr-Wold device and Theorem 5.9 to the right-hand side of (6.49) we obtain the following theorem. a na