Questions:
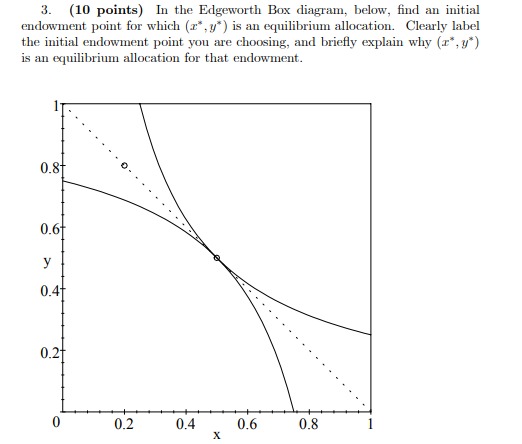
1. (10 points) Suppose that there are two goods, x and y, and that x is an inferior good. Show as precisely as you can why good y must be a normal good.2. (10 points) True or false, and explain: The income effect on the demand for gasoline, when the price of gasoline increases from $1.50 to $1.60. is likely to be greater for someone who drives a lot than for someone who does not drive very much. (Give a verbal explanation. You do not have to graph this.)3. (10 points) In the Edgeworth Box diagram, below, find an initial endowment point for which (2*, y* ) is an equilibrium allocation. Clearly label the initial endowment point you are choosing, and briefly explain why (a*, y*) is an equilibrium allocation for that endowment. 0.8+ 0.6+ 0.4+ 0.21 0 0.2 0.4 0.6 0.8 X4. (20 points) The Buckeye Corporation sells OSU t-shirts in Columbus and in Cincinnati. Marketing research has indicated that the demand for t- shirts in Columbus, Teal, is given by the function Tool = 4800 - 200p. and that the demand for t-shirts in Cincinnati, Crime, is given by the function cine = 3200 - 100p, where p refers to the price of t-shirts. Assume that the same price must be charged in both cities. (a) What is Buckeye's statewide demand function, when we aggregate the demands in the two cities into a single, statewide market? (b) If the price elasticity of demand in the Columbus market is -I (unitary elasticity), how many t-shirts are demanded in Columbus, and how many t-shirts are demanded in Cincinnati?5. (20 points) A consumer has the utility function over goods x and y, u(r, y) = xyl/2 Suppose this consumer has an income of 12, M = 12. Let the price of good x be 4, pr = 4, and let the price of good y be 1, py = 1. Calculate the bundle of goods I and y that maximizes this consumer's utility, subject to her budget constraint.6. (30 points) Xavier's Xylophone Repair uses capital and labor to provide xylophone repair services, according to the production function, T = KL1/2. where x is the quantity of xylophones repaired, K is the quantity of capital used, and L is the quantity of labor used. (a) Does this production function exhibit decreasing returns to scale, con- stant returns to scale, or increasing returns to scale? Explain. (b) Does this production function exhibit diminishing marginal returns to labor? Explain. (Problem 6, parts c and d, continued on next page.) (c) If the price of labor is 1, w=1, and the price of capital is 2, r=2, derive the long run total cost function (that is, total cost as a function of output, c). (d) Suppose that we are in a short run situation in which the capital input is fixed at 10, K = 10. If the price of labor is 1, w=1, and the price of capital is 2. r=2, derive the short run average total cost function