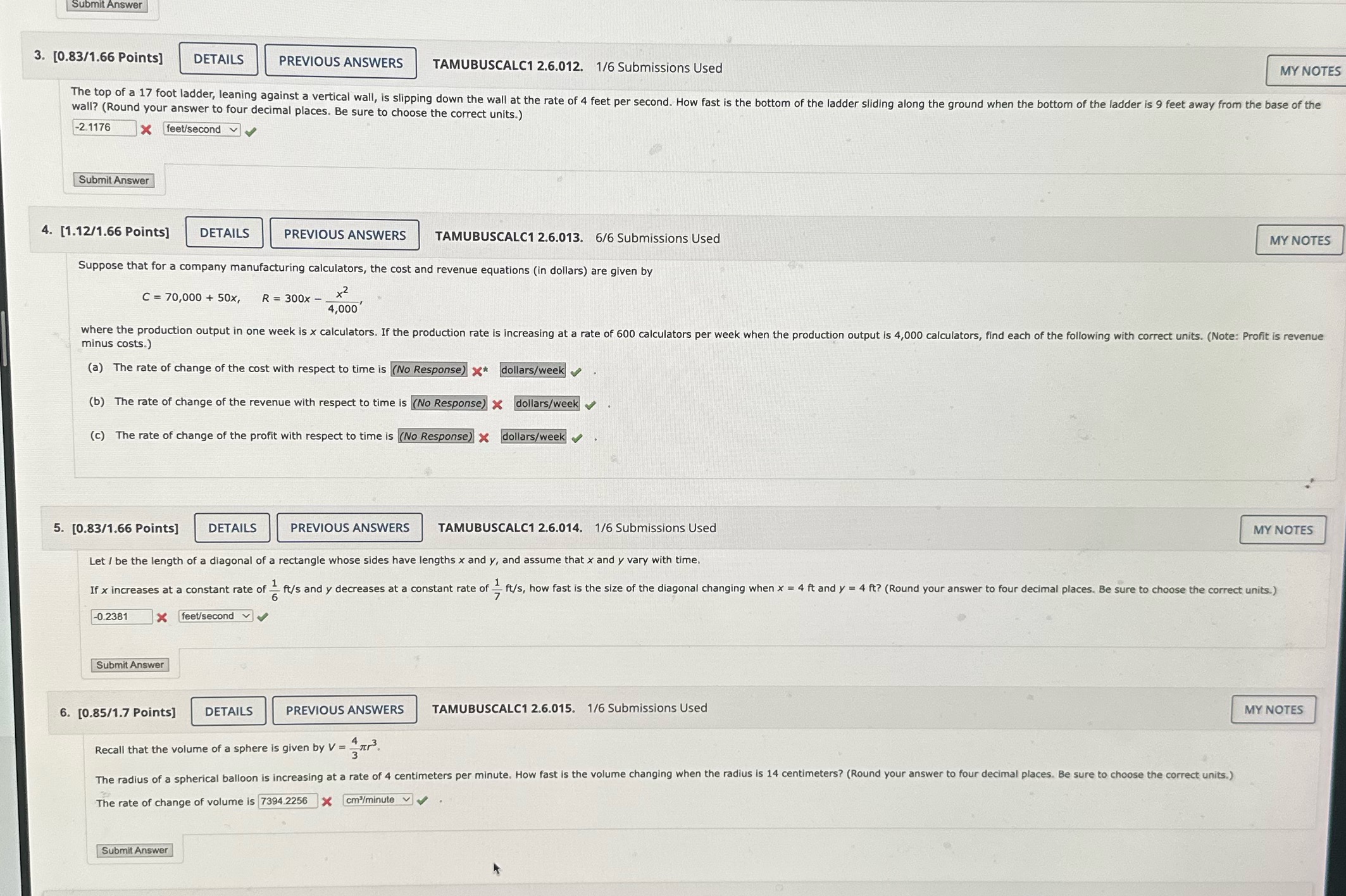
questions 3, 5, 6 please

Submit Answer 3. [0.83/1.66 Points] DETAILS PREVIOUS ANSWERS TAMUBUSCALC1 2.6.012. 1/6 Submissions Used MY NOTES The top of a 17 foot ladder, leaning against a vertical wall, is slipping down the wall at the rate of 4 feet per second. How fast is the bottom of the ladder sliding along the ground when the bottom of the ladder is 9 feet away from the base of the wall? (Round your answer to four decimal places. Be sure to choose the correct units.) -2.1176 * feet/second Submit Answer 4. [1.12/1.66 Points] DETAILS PREVIOUS ANSWERS TAMUBUSCALC1 2.6.013. 6/6 Submissions Used MY NOTES Suppose that for a company manufacturing calculators, the cost and revenue equations (in dollars) are given by C = 70,000 + 50x, R = 300x - 4,000 where the production output in one week is x calculators. If the production rate is increasing at a rate of 600 calculators per week when the production output is 4,000 calculators, find each of the following with correct units. (Note: Profit is revenue minus costs.) (a) The rate of change of the cost with respect to time is (No Response) x* dollars/week (b) The rate of change of the revenue with respect to time is (No Response) x dollars/week (c) The rate of change of the profit with respect to time is (No Response) x dollars/week 5. [0.83/1.66 Points] DETAILS PREVIOUS ANSWERS TAMUBUSCALC1 2.6.014. 1/6 Submissions Used MY NOTES Let / be the length of a diagonal of a rectangle whose sides have lengths x and y, and assume that x and y vary with time. If x increases at a constant rate of - ft/s and y decreases at a constant rate of - ft/s, how fast is the size of the diagonal changing when x = 4 ft and y = 4 ft? (Round your answer to four decimal places. Be sure to choose the correct units.) -0.2381 x feet/second Submit Answer 6. [0.85/1.7 Points] DETAILS PREVIOUS ANSWERS TAMUBUSCALC1 2.6.015. 1/6 Submissions Used MY NOTES Recall that the volume of a sphere is given by V = 473 The radius of a spherical balloon is increasing at a rate of 4 centimeters per minute. How fast is the volume changing when the radius is 14 centimeters? (Round your answer to four decimal places. Be sure to choose the correct units.) The rate of change of volume is 7394.2256 x cm /minute Submit