Quip Corporation wants to purchase a new machine for $385,000. Management predicts that the machine will produce sales of $290,000 each year for the next 5 years. Expenses are expected to include direct materials, direct labor, and factory overhead (excluding depreciation) totaling $89,000 per year. The firm uses straight-line depreciation with an assumed residual (salvage) value of $50,000. Quip's combined income tax rate, t, is 40%.
Management requires a minimum after-tax rate of return of 10% on all investments. What is the approximate internal rate of return (IRR) of the proposed investment? (Note: To answer this question, students must have access to Table 2 from Appendix C, Chapter 12.) Assume that all cash flows occur at year-end.
Multiple Choice
-
Less than 22%.
-
Somewhere between 25% and 30%.
-
Somewhere between 24% and 25%.
-
Over 30%.
-
Somewhere between 22% and 24%.
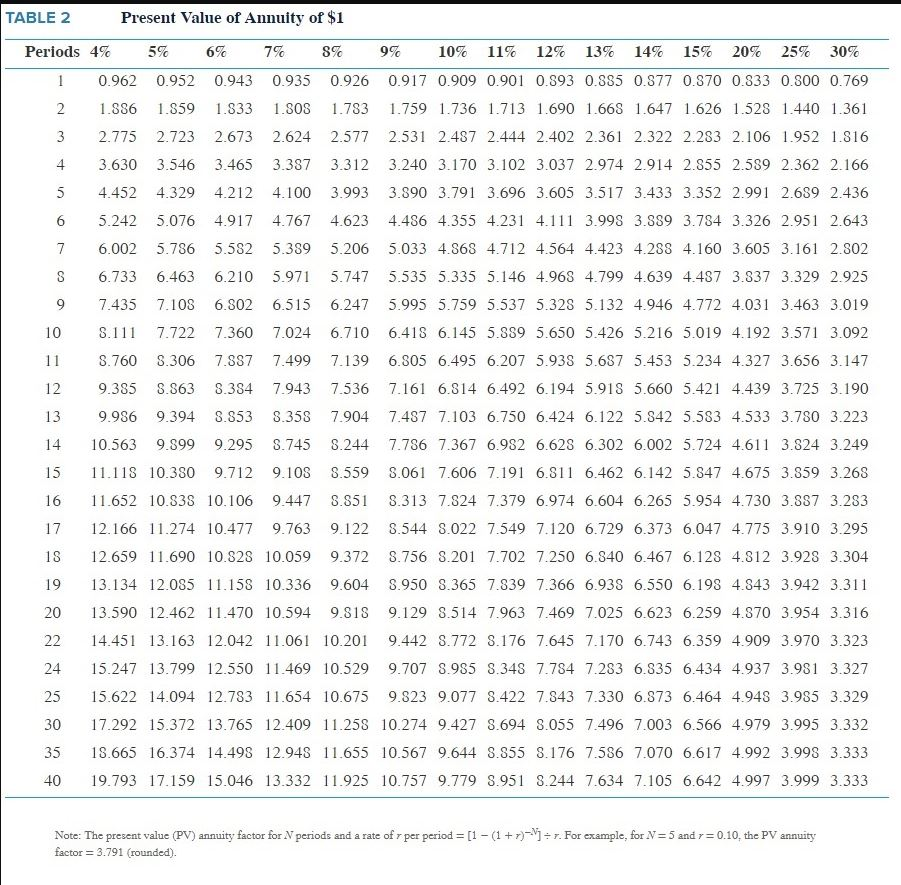
TABLE 2 Present Value of Annuity of $1 Periods 4% 5% 6% 7% 8% 9% 10% 11% 12% 13% 14% 15% 20% 25% 30% 0.962 0.952 0.943 0.935 0.926 0.917 0.909 0.901 0.893 0.385 0.877 0.370 0.333 0.500 0.769 1.836 1.559 1.833 1.30S 1.783 1.759 1.736 1.713 1.690 1.668 1.647 1.626 1.528 1.440 1.361 2.775 2.723 2.673 2.624 2.577 2.531 2.487 2.444 2.402 2.361 2.322 2.283 2.106 1.952 1.816 3.630 3.546 3.465 3.387 3.312 3.240 3.170 3.102 3.037 2.974 2.914 2.355 2.589 2.362 2.166 4.452 4.329 4.212 4.100 3.993 3.890 3.791 3.696 3.605 3.517 3.433 3.352 2.991 2.689 2.436 5.242 5.076 4.917 4.767 4.623 4.486 4.355 4.231 4.111 3.998 3.889 3.784 3.326 2.951 2.643 6.002 5.786 5.582 5.389 5.206 5.033 4.363 4.712 4.564 4.423 4.288 4.160 3.605 3.161 2.802 6.733 6.463 6.210 5.971 5.747 5.535 5.335 5.146 4.968 4.799 4.639 4.487 3.837 3.329 2.925 7.435 7.108 6.802 6.515 6.247 5.995 5.759 5.537 5.328 5.132 4.946 4.772 4.031 3.463 3.019 8.111 7.722 7.360 7.024 6.710 6.418 6.145 5.889 5.650 5.426 5.216 5.019 4.192 3.571 3.092 8.760 5.306 7.887 7.499 7.139 6.805 6.495 6.207 5.939 5.687 5.453 5.234 4.327 3.656 3.147 9.385 .863 8.354 7.943 7.536 7.161 6.314 6.492 6.194 5.918 5.660 5.421 4.439 3.725 3.190 9.986 9.394 3.353 3.358 7904 7.487 7.103 6.750 6.424 6.122 5.342 5.553 4.533 3.780 3.223 10.563 9.999 9.295 8.745 8.244 7.736 7.367 6.982 6.628 6.302 6.002 5.724 4.611 3.324 3.249 15 11.118 10.380 9.712 9.108 3.559 .061 7.606 7.191 6.811 6.462 6.142 5.347 4.675 3.359 3.268 16 11.652 10.838 10.106 9.447 8.551 8.313 7.824 7.379 6.974 6.604 6.265 5.954 4.730 3.887 3.283 17 12.166 11.274 10.477 9.763 9.122 8.544 3.022 7.549 7.120 6.729 6.373 6.047 4.775 3.910 3.295 13 12.659 11.690 10.528 10.059 9.372 3.756 3.201 7.702 7.250 6.340 6.467 6.128 4.812 3.928 3.304 19 13.134 12.085 11.158 10.336 9.604 S.950 8.365 7.839 7.366 6.938 6.550 6.198 4.343 3.942 3.311 20 13.590 12.462 11.470 10.594 9.818 9.129 8.514 7.963 7.469 7.025 6.623 6.259 4.370 3.954 3.316 22 14.451 13.163 12.042 11.061 10.201 9.442 8.772 8.176 7.645 7.170 6.743 6.359 4.909 3.970 3.323 24 15.247 13.799 12.550 11.469 10.529 9.707 8.985 3.343 7.784 7.283 6.335 6.434 4.937 3.981 3.327 15.622 14.094 12.783 11.654 10.675 9.823 9.077 8.422 7.843 7.330 6.573 6.464 4.948 3.985 3.329 30 17.292 15.372 13.765 12.409 11.258 10.274 9.427 8.694 8.055 7.496 7.003 6.566 4.979 3.995 3.332 35 15.665 16.374 14.498 12.948 11.655 10.567 9.644 8.555 8.176 7.586 7.070 6.617 4.992 3.998 3.333 40 19.793 17.159 15.046 13.332 11.925 10.757 9.779 5.951 8.244 7.634 7.105 6.642 4.997 3.999 3.333 Note: The present value (PV) annuity factor for N periods and a rate of r per period = [1 - (1 + r)-Y] = r. For example, for N=5 and r=0.10, the PV annuity factor = 3.791 (rounded)







