Ralphs cost curve is piece-wise linear. For output of 0 q 1,000 units it is given by C(q;P) = 1,000 + 6q; for 1,000 q 2,000 it is given by C(q;P) = 3,000 + 4q; and for 2,000 q it is given by C(q;P) = 5,000 + 8q. Assume the selling price is 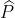= 7, with break-even being q=1000

(a) Now approximate Ralphs cost curve with an LLA of 3,000+4q; notice this approximation is consistent with the optimal output chosen above as well as the original break-even calculation. Suppose the selling price unexpectedly drops to 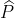= 4.8. Using the LLA of 3,000 + 4q, calculate Ralphs best choice of output (somewhere between shutdown and a maximum of 2,000 units). (b) What mistake has Ralph made in part (a) above?

I'm uncertain how to do these two tasks. Please help with a step-by-step solution for the above